Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Chọn A
+ Ba số x + 6 y ,5 x + 2 y ,8 x + y lập thành cấp số cộng nên
x + 6 y + 8 x + y = 2 5 x + 2 y ⇔ 9 x + 7 y = 10 x + 4 y ⇔ x = 3 y
+ Ba số x + 5 3 , y − 1,2 x − 3 y lập thành cấp số nhân nên x + 5 3 2 x − 3 y = y − 1 2 .
Thay x= 3y vào ta được :
3 y + 5 3 2.3 y − 3 y = y − 1 2 ⇔ 3 y + 5 3 .3 y = y 2 − 2 y + 1 ⇔ 9 y 2 + 5 y − y 2 + 2 y − 1 = 0
⇔ 8 y 2 + 7 y − 1 = 0 ⇔ y = − 1 hoặc y = 1 8 .
Với y= -1 thì x= - 3; với y = 1 8 thì x = 3 8 .
Ta có hệ phương trình:
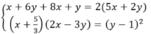
Từ đó ta suy ra
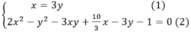
Thế (1) vào (2) ta được: 8y2+7y-1=0⇒y=-1 hoặc y=1/8
Do y < 0 , ta được y = -1, x = -3
Đáp án B
Chọn B
Từ 8 x , 4 x , 2 theo thứ tự lập thành một cấp số nhân nên công bội q = 2 4 4 = 1 2 7
Suy ra 4 4 = 8 x . 1 2 7 ⇒ x = 5
Mặt khác log 2 45 , log 2 y , log 2 x theo thứ tự lập thành cấp số cộng suy ra
⇔ log 2 y = log 2 45 + log 2 5 : 2
⇔ log 2 y = log 2 225
⇔ y = 15
Chọn A
Theo giả thiết ta có :
y = x q ; z = x q 2 x + 3 z = 2 2 y ⇒ x + 3 x q 2 = 4 x q ⇒ x 3 q 2 − 4 q + 1 = 0 ⇔ x = 0 3 q 2 − 4 q + 1 = 0 .
Nếu x = 0 ⇒ y = z = 0 ⇒ công sai của cấp số cộng: x ; 2y ; 3z bằng 0 (vô lí).
nếu
3 q 2 − 4 q + 1 = 0 ⇔ q = 1 q = 1 3 ⇔ q = 1 3 q = 1 .
Chọn A.
Phương pháp:
Ba số x, y, z lập thành một cấp số cộng
⇔ x + z - 2 y
Và số x, y, z lập thành một cấp số nhân ⇔ x z = y 2
Cách giải
Do 3 số x, y, z lập thành một cấp số cộng và có tổng bằng 21 nên ta có
x + z = 2 y x + y + z = 21
⇔ x + z = 14 y = 7
⇔ x = 14 - z y = 7 ( 1 )
Nếu lần lượt thêm các số 2; 3; 9 vào ba số đó (theo thứ tự của cấp số cộng)
thì được ba số lập thành một cấp số nhân nên ta có
( x + 2 ) ( z + 9 ) = ( y + 3 ) 2 ( 2 )
Thay (1) vào (2) ta có:
( 14 - z + 2 ) ( z + 9 ) = ( 7 + 3 ) 2
⇔ z 2 - 7 z - 44 = 0
⇔ z = 11 z = - 4
z = 11 ⇒ z = 14 - 11 = 3
⇒ F = x 2 + y 2 + z 2 = 179
z = - 4 ⇒ x = 14 - ( - 4 ) = 18
⇒ F = x 2 + y 2 + z 2 = 389
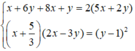
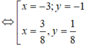
Theo giả thiết ta có x + 6 y + 8 x + y = 2 5 x + 2 y x − 1 x − 3 y = y + 2 2
⇔ x = 3 y 3 y − 1 3 y − 3 y = y + 2 2 ⇔ x = 3 y 0 = y + 2 2 ⇔ x = − 6 y = − 2 .
Suy ra x 2 + y 2 = 40.
Chọn đáp án A.