Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
A B C A' B' C' a)Do A',B',C' là trung điểm BC,CA,AB=> A'B' song song với AB,B'C'song song với BC,C'A' song song với CA
\(\overrightarrow{A'B'}=\left(6;3\right)\) => VTPT của đường thẳng AB là: \(\overrightarrow{n}=\left(1;-2\right)\)
và C' thuộc (AB)=>Phương trình đường thẳng AB là:
(AB): x-2y-6=0
Tương tự ta có phương trình đường thẳng BC là:
(BC): x+4=0
Tọa độ điểm B là nghiệm hệ
\(\left\{{}\begin{matrix}\text{x-2y-6=0}\\x+4=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-4\\y=-5\end{matrix}\right.\)
=>B(-4;-5)
A'(-4;1) là TĐ của BC => tọa độ C(-4;7)
C'(2;-2) là TĐ của AB =>tọa độ A(8;1)
b) Gọi tọa độ trọng tâm G của tam giác A'B'C' là G(x;y)
=>\(\overrightarrow{GA'}+\overrightarrow{GB'}+\overrightarrow{GC'}=0\)
=>\(\left\{{}\begin{matrix}\left(-4-x\right)+\left(2-x\right)+\left(2-x\right)=0\\\left(1-y\right)+\left(4-y\right)+\left(-2-y\right)=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=0\\y=1\end{matrix}\right.\)
=>G(0;1)
Thay vào tính
Ta có:\(\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}\) =(8-4-4;1-1+7-1-5-1)=(0;0)
=>G là trọng tâm tam giác ABC=>ĐPCM
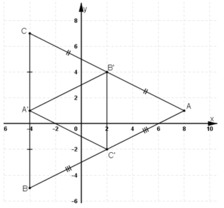
A’ là trung điểm của BC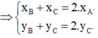 
B’ là trung điểm của AC 
C’ là trung điểm của BA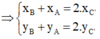 
Gọi G là trọng tâm ΔABC và G’ là trọng tâm ΔA’B’C’
Ta có :
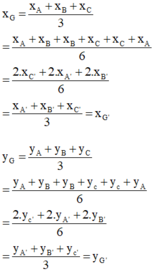
Vậy G ≡ G’ (đpcm)
a) Gọi tọa độ các điểm như sau: \(A\left( {{x_A};{y_A}} \right),B\left( {{x_B};{y_B}} \right),C\left( {{x_C};{y_C}} \right)\)
\(M\left( {2;2} \right),N\left( {3;4} \right),P\left( {5;3} \right)\) lần lượt là trung điểm của các cạnh AB, BC và CA nên ta có:
\(\left\{ \begin{array}{l}{x_A} + {x_B} = 2{x_M}=4\\{x_A} + {x_C} = 2{x_P}=10\\{x_C} + {x_B} = 2{x_N}=6\\{y_A} + {y_B} = 2{y_M}=4\\{y_A} + {y_C} = 2{y_P}=8\\{y_C} + {y_B} = 2{y_N}=6\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{x_A} + {x_B} = 4\\{x_C} - {x_B} = 6\\{x_C} + {x_B} = 6\\{y_A} + {y_B} = 4\\{y_C} - {y_B} = 4\\{y_C} + {y_B} = 6\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{x_A} = 4\\{x_B} = 0\\{x_C} = 6\\{y_A} = 3\\{y_B} = 1\\{y_C} = 5\end{array} \right.\)
Vậy các đỉnh của tam giác có tọa độ là \(A\left( {4;3} \right),B\left( {0;1} \right),C\left( {6;5} \right)\)
b) Gọi \(G\left( {{x_G};{y_G}} \right),G'\left( {{x_{G'}};{y_{G'}}} \right)\) là trọng tâm của hai tam giác ABC và MNP
Áp dụng tính chất trọng tâm ta có:
\(\begin{array}{l}{x_G} = \frac{{{x_A} + {x_B} + {x_C}}}{3} = \frac{{4 + 0 + 6}}{3} = \frac{{10}}{3};{y_G} = \frac{{{y_A} + {y_B} + {y_C}}}{3} = \frac{{3 + 1 + 5}}{3} = 3\\{x_{G'}} = \frac{{{x_M} + {x_N} + {x_P}}}{3} = \frac{{2 + 3 + 5}}{3} = \frac{{10}}{3};{y_{G'}} = \frac{{{y_M} + {y_N} + {y_P}}}{3} = \frac{{2 + 4 + 3}}{3} = 3\end{array}\)
Suy ra \(G\left( {\frac{{10}}{3};3} \right)\) và \(G'\left( {\frac{{10}}{3};3} \right)\), tọa độ của chúng bằng nhau nên hai điểm G và G’ trùng nhau (đpcm)
c) Ta có: \(\overrightarrow {AB} = \left( { - 4; - 2} \right),\overrightarrow {AC} = \left( {2;2} \right),\overrightarrow {BC} = \left( {6;4} \right)\)
Suy ra: \(AB = \left| {\overrightarrow {AB} } \right| = \sqrt {{{( - 4)}^2} + {{( - 2)}^2}} = 2\sqrt 5 ,AC = \left| {\overrightarrow {AC} } \right| = \sqrt {{2^2} + {2^2}} = 2\sqrt 2 \)
\(BC = \left| {\overrightarrow {BC} } \right| = \sqrt {{6^2} + {4^2}} = 2\sqrt {13} \)
\(\begin{array}{l}\cos A = \cos \left( {\overrightarrow {AB} ,\overrightarrow {AC} } \right) = \frac{{\overrightarrow {AB} .\overrightarrow {AC} }}{{AB.AC}} = \frac{{( - 4).2 + ( - 2).2}}{{2\sqrt 5 .2\sqrt 2 }} = - \frac{{3\sqrt {10} }}{{10}} \Rightarrow \widehat A \approx 161^\circ 33'\\\cos B = \cos \left( {\overrightarrow {BA} ,\overrightarrow {BC} } \right) = \frac{{\overrightarrow {BA} .\overrightarrow {BC} }}{{BA.BC}} = \frac{{4.6 + 2.4}}{{2\sqrt 5 .2\sqrt {13} }} = \frac{{8\sqrt {65} }}{{65}} \Rightarrow \widehat B = 7^\circ 7'\\\widehat C = 180^\circ - \widehat A - \widehat B = 180^\circ - 161^\circ 33' - 7^\circ 7' = 11^\circ 20'\end{array}\)
A B C M N P
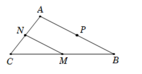
Gọi \(A\left(x_A;y_A\right);B\left(x_B;y_B\right);C\left(x_C;y_C\right)\).
\(\overrightarrow{MN}\left(1;2\right)\); \(\overrightarrow{BP}\left(-x_B;-4-y_B\right)\).
MN là đường trung bình của tam giác ABC nên: \(\overrightarrow{MN}=\dfrac{1}{2}\overrightarrow{BC}=\overrightarrow{BN}\).
Vì vậy \(\left\{{}\begin{matrix}-x_B=1\\-4-y_B=2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x_B=-1\\y_B=-6\end{matrix}\right.\)\(\Leftrightarrow B\left(-1;-6\right)\).
\(\overrightarrow{NP}\left(-2;-7\right)\); \(\overrightarrow{AM}\left(1-x_A;1-y_A\right)\).
NP là đường trung bình của tam giác ABC nên:
\(\overrightarrow{NP}=\dfrac{1}{2}\overrightarrow{AB}=\overrightarrow{AM}\).
Vì vậy \(\left\{{}\begin{matrix}1-x_A=-2\\1-y_A=-7\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}x_A=3\\y_A=8\end{matrix}\right.\)\(\Rightarrow A\left(3;8\right)\).
Do M là trung điểm của AB nên:
\(\dfrac{x_A+x_B}{2}=x_M\Rightarrow x_B=2x_M-x_A=2.1-3=-1\).
\(\dfrac{y_A+y_B}{2}=y_M\Rightarrow y_B=2y_M-y_A=2.1-8=-6\).
Vậy \(B\left(-1;-6\right)\).
bạn ơi, cách làm của bạn thì ok lắm nhưng theo mình thì có vẻ bạn đang nhầm đề bài á??... ví dụ ở đề bài M là trung điểm của BC nhưng trong hình vẽ của bạn điểm M lại là trung điểm của AB mất rồi!!! Đó là suy nghĩ của mình thoii, nếu như không hợp lý thì mình xin lỗi :))
Theo tích chất đường trung bình trong một tam giác ta có: \(\overrightarrow {PN} = \overrightarrow {BM} = \overrightarrow {MC} \) và \(\overrightarrow {MP} = \overrightarrow {NA} \)
Gọi \(A\left( {{a_1},{a_2}} \right),B\left( {{b_1};{b_2}} \right),C\left( {{c_1};{c_2}} \right)\)
Ta có: \(\overrightarrow {PN} = \left( {2;3} \right)\),\(\overrightarrow {BM} = \left( {1 - {b_1}; - 2 - {b_2}} \right)\), \(\overrightarrow {MC} = \left( {{c_1} - 1;{c_2} + 2} \right)\), \(\overrightarrow {MP} = \left( {5;4} \right)\), \(\overrightarrow {NA} = \left( {{a_1} - 4;{a_2} + 1} \right)\)
Có \(\overrightarrow {PN} = \overrightarrow {BM} \Leftrightarrow \left\{ \begin{array}{l}2 = 1 - {b_1}\\3 = - 2 - {b_2}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{b_1} = - 1\\{b_2} = - 5\end{array} \right.\) .Vậy \(B\left( { - 1; - 5} \right)\)
Có \(\overrightarrow {PN} = \overrightarrow {MC} \Leftrightarrow \left\{ \begin{array}{l}2 = {c_1} - 1\\3 = {c_2} + 2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{c_1} = 3\\{c_2} = 1\end{array} \right.\) .Vậy \(C\left( {3;1} \right)\)
Có \(\overrightarrow {NA} = \overrightarrow {MP} \Leftrightarrow \left\{ \begin{array}{l}5 = {a_1} - 4\\4 = {a_2} + 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{a_1} = 9\\{a_2} = 3\end{array} \right.\) .Vậy \(A\left( {9;3} \right)\)
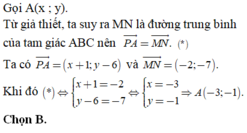
A’ là trung điểm của cạnh BC nên -4 =
(xB+ xC)
=> xB+ xC = -8 (1)
Tương tự ta có xA+ xC = 4 (2)
xB+ xC = 4 (3)
=> xA+ xB+ xC =0 (4)
Kết hợp (4) và (1) ta có: xA= 8
(4) và (2) ta có: xB= -4
(4) và (3) ta có: xC = -4
Tương tự ta tính được: yA = 1; yB = -5; yC = 7.
Vậy A(8;1), B(-4;-5), C(-4; 7).
Gọi G la trọng tâm tam giác ABC thì
xG=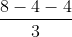
= 0; yG = 
= 1 => G(0,1).
xG’=
; yG’ = 
= 1 => G'(0;1)
Rõ ràng G và G’ trùng nhau.