
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bài 3:
b: \(B_1=-\left|2x-3\right|+2\le2\forall x\)
Dấu '=' xảy ra khi \(x=\dfrac{3}{2}\)
\(B_2=-\left|x+4\right|+5\le5\forall x\)
Dấu '=' xảy ra khi x=-4
Bài 3:
b) Xét số \(-B_3=6+\left|x+4\right|\ge6\Rightarrow B_3\le-6\)
Dấu '=' xảy ra \(\Leftrightarrow x=-4\)

\(1,\\ a,A_1=\left(x-2\right)^2+5\ge5\)
Dấu \("="\Leftrightarrow x=2\)
\(A_2=\left(x+1\right)^2+7\ge7\)
Dấu \("="\Leftrightarrow x=-1\)
\(A_3=\left(3-2x\right)^2-1\ge-1\)
Dấu \("="\Leftrightarrow x=\dfrac{3}{2}\)
\(A_4=\left(x-2\right)^2-3\ge-3\)
Dấu \("="\Leftrightarrow x=2\)
\(b,B_1=\left|x-2\right|+3\ge3\)
Dấu \("="\Leftrightarrow x=2\)
\(B_2=\left|x+1\right|+3\ge3\)
Dấu \("="\Leftrightarrow x=-1\)
\(B_3=\left|2x-4\right|-3\ge-3\)
Dấu \("="\Leftrightarrow x=2\)
\(B_4=\left|6x+1\right|-20\ge-20\)
Dấu \("="\Leftrightarrow x=-\dfrac{1}{6}\)
Bài 1:
a: \(A_1=\left(x-2\right)^2+5\ge5\forall x\)
Dấu '=' xảy ra khi x=2
\(A_2=\left(x+1\right)^2+7\ge7\forall x\)
Dấu '=' xảy ra khi x=-1
\(A_3=\left(3-2x\right)^2-1\ge-1\forall x\)
Dấu '=' xảy ra khi \(x=\dfrac{3}{2}\)
\(A_4=\left(x-2\right)^2-3\ge-3\forall x\)
Dấu '=' xảy ra khi x=2

Bài 2:
Đặt \(\frac{a}{b}=\frac{c}{d}=k\Rightarrow\begin{cases}a=kb\\c=kd\end{cases}\)
=> \(\frac{5a+3b}{5a-3b}=\frac{5kb+3b}{5kb-3b}=\frac{b\left(5k+3\right)}{b\left(5k-3\right)}=\frac{5k+3}{5k-3}\left(1\right)\)
\(\frac{5c+3d}{5c-3d}=\frac{5kd+3d}{5kd-3d}=\frac{d\left(5k+3\right)}{d\left(5k-3\right)}=\frac{5k+3}{5k-3}\left(2\right)\)
Từ (1) và (2) => \(\frac{5a+3b}{5a-3b}=\frac{5c+3d}{5c-3d}\)
Bài 3:
Đặt \(\frac{a}{b}=\frac{b}{c}=\frac{c}{d}=k\)
=> \(\frac{a}{b}.\frac{b}{c}.\frac{c}{d}=k^3\)
=> \(\frac{a}{d}=k^3\) (1)
Lại có: \(\frac{a+b+c}{b+c+d}=\frac{a}{b}=\frac{b}{c}=\frac{c}{d}=k\)
=> \(\left(\frac{a+b+c}{b+c+d}\right)^3=k^3\) (2)
Từ (1) và (2) => \(\frac{a}{d}=\left(\frac{a+b+c}{b+c+d}\right)^3\)

Lần sau bạn nhớ đánh đề rõ ràng hơn. Nếu nhìn đề thì mình nghĩ thế này
 Các bạn giúp mk mỗi bài 2 phần b hoi ạ
Các bạn giúp mk mỗi bài 2 phần b hoi ạ Các bạn giúp mk mỗi bài 3 phần b với phần c hoi ạ><
Các bạn giúp mk mỗi bài 3 phần b với phần c hoi ạ><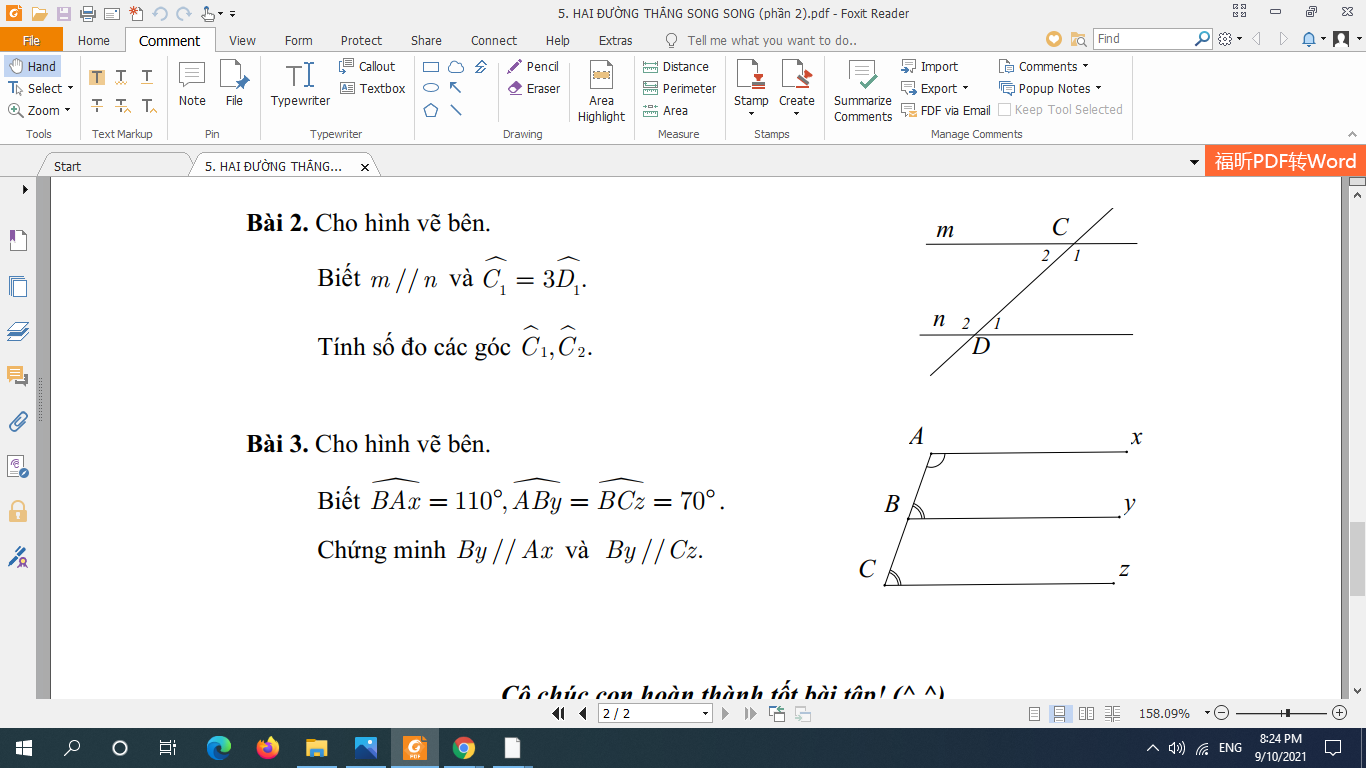 Các cậu làm hộ mk mỗi bài 3 hoi ạ:33
Các cậu làm hộ mk mỗi bài 3 hoi ạ:33 Các bạn giúp mk mỗi bài 1 hoi ạ:))
Các bạn giúp mk mỗi bài 1 hoi ạ:))
Bài 2
b)\(B_1=\left(x-3\right)^2+\left|y+1\right|\ge0\)
dấu '=' xảy ra \(\Leftrightarrow\left\{{}\begin{matrix}x=3\\y=-1\end{matrix}\right.\)
c) \(B_2=\left(x-y\right)^2+\left(3x+1\right)^2-3\ge-3\)
Dấu '=' xảy ra \(\Leftrightarrow\left\{{}\begin{matrix}x=-\dfrac{1}{3}\\y=\dfrac{-1}{3}\end{matrix}\right.\)