K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
AH
Akai Haruma
Giáo viên
2 tháng 12 2023
Bạn nên viết đề bằng công thức toán (biểu tượng $\sum$ góc trái khung soạn thảo) để mọi người hiểu đề của bạn hơn. Viết ntn khá khó đọc.
làm giúp mình bài 3 vớiiii :<
NV
Nguyễn Việt Lâm
Giáo viên
21 tháng 12 2022
\(\overrightarrow{AB}.\overrightarrow{AC}=AB.AC.cos\widehat{BAC}=a.a.cos60^0=\dfrac{a^2}{2}\)
\(\overrightarrow{AB}.\overrightarrow{AM}=AB.AM.cos\widehat{BAM}=a.\dfrac{a\sqrt{3}}{2}.cos30^0=\dfrac{3a^2}{4}\)
\(\overrightarrow{AB}.\overrightarrow{BC}=AB.BC.cos\left(180^0-\widehat{ABC}\right)=a.a.cos120^0=-\dfrac{a^2}{2}\)
\(\overrightarrow{AC}.\overrightarrow{BM}=\overrightarrow{AC}.\dfrac{1}{2}\overrightarrow{BC}=\dfrac{1}{2}AC.BC.cos\widehat{ACB}=\dfrac{1}{2}a.a.cos60^0=\dfrac{a^2}{4}\)
NV
Nguyễn Việt Lâm
Giáo viên
3 tháng 3 2022
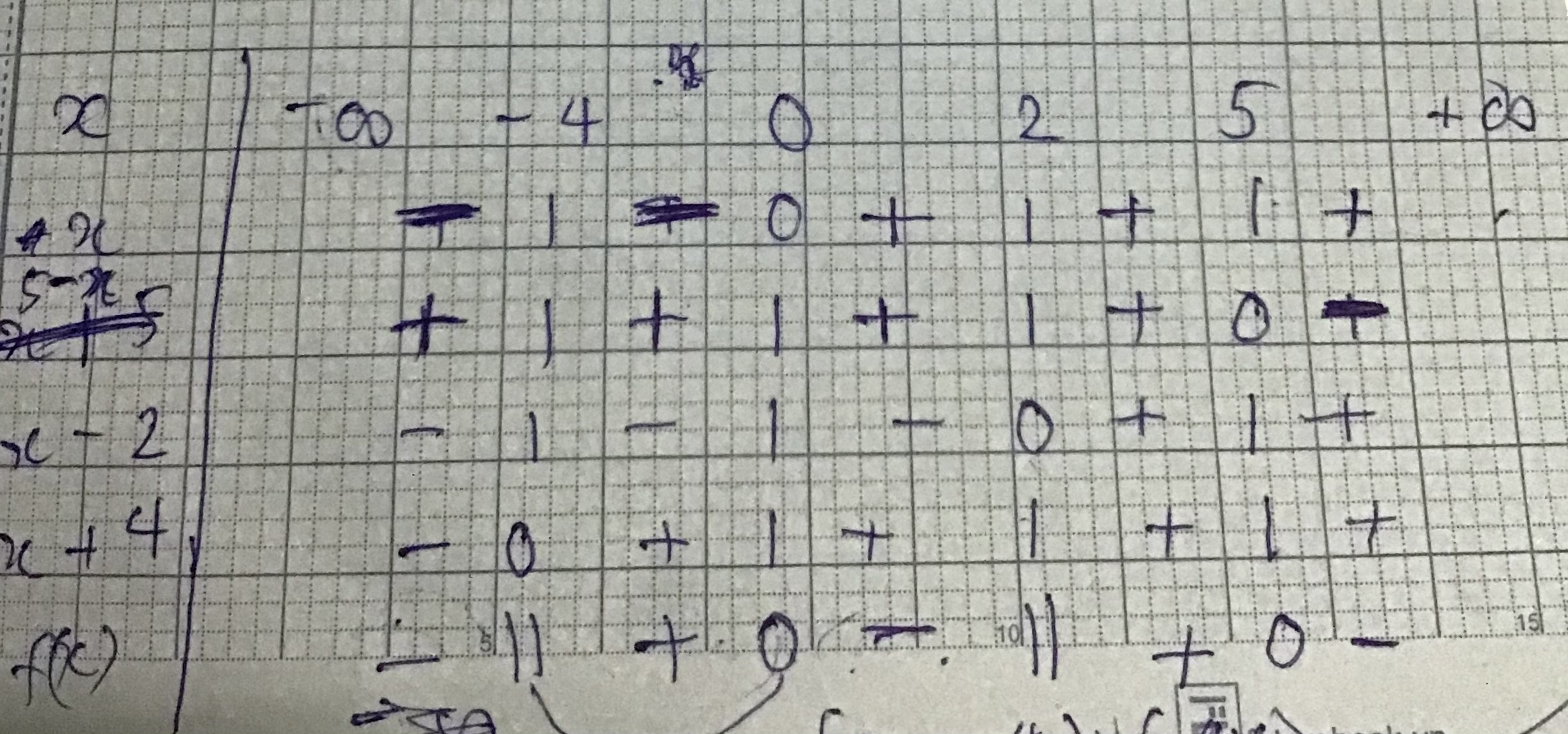
Giữ nguyên bình phương và xét dấu như bình thường
Em bỏ bình phương nên xét dấu bị sai dẫn đến kết quả sai
NH
1
KL
1
AH
Akai Haruma
Giáo viên
30 tháng 1 2017
Lời giải:
GTLN:
Áp dụng BĐT Cauchy-Schwarz:
\(B^2=(6\sqrt{x-1}+8\sqrt{3-x})^2\leq (6^2+8^2)(x-1+3-x)=200\)
\(\Rightarrow B_{\max}= 10\sqrt{2}\Leftrightarrow \frac{3}{\sqrt{x-1}}=\frac{4}{\sqrt{3-x}}\Leftrightarrow x=\frac{43}{25}\)
GTNN:
Ta biết một bổ đề sau: Với \(a,b\geq 0\Rightarrow \sqrt{a}+\sqrt{b}\geq \sqrt{a+b}\)
Cách CM rất đơn giản vì nó tương đương với \(\sqrt{ab}\geq 0\) (luôn đúng)
Áp dụng vào bài toán:
\(\Rightarrow B\geq \sqrt{36x-36+192-64x}=\sqrt{156-28x}\geq 6\sqrt{2}\) (do \(x\leq 3\))
Vậy \(B_{\min}=6\sqrt{2}\Leftrightarrow x=3\)
16 tháng 5 2023
4:
\(n\left(\Omega\right)=C^3_{35}\)
\(n\left(A\right)=C^3_{15}\)
=>\(P\left(A\right)=\dfrac{13}{187}\)
Để B ⊂ A thì:
1 - 2m ≤ -3 và m + 1 ≥ 5
*) -1 - 2m ≤ -3
⇔ -2m ≤-3 + 1
⇔ -2m ≤ -2
⇔ m ≥ 1 (1)
*) m + 1 ≥ 5
⇔ m ≥ 5 - 1
⇔ m ≥ 4 (2)
Từ (1) và (2) ⇒ m ≥ 4
Vậy m ≥ 4 thì B ⊂ A