
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



1:
a: Khi m=1 thì (1) sẽ là x^2+2x-5=0
=>\(x=-1\pm\sqrt{6}\)
b: Δ=(2m)^2-4(-2m-3)
=4m^2+8m+12
=4m^2+8m+4+8=(2m+2)^2+8>=8>0
=>Phương trình luôn có hai nghiệm phân biệt
2:
Thay x=-1 và y=2 vào (P), ta được:
a*(-1)^2=2
=>a=2

b: Xét ΔAHC vuông tại H có HM là đường cao
nên \(AM\cdot AC=AH^2\left(1\right)\)
Xét ΔABC vuông tại A có AH là đường cao
nên \(HB\cdot HC=AH^2\left(2\right)\)
Từ (1) và (2) suy ra \(AM\cdot AC=HB\cdot HC\)

\(a,=\left(\sqrt{a}-1\right)\left(a+\sqrt{a}+1\right)\\ b,=\left(\sqrt{x}-\sqrt{y}\right)\left(\sqrt{x}+\sqrt{y}\right)-2\left(\sqrt{x}+\sqrt{y}\right)\\ =\left(\sqrt{x}+\sqrt{y}\right)\left(\sqrt{x}-\sqrt{y}-2\right)\\ c,=x\left(\sqrt{x}-1\right)-\left(\sqrt{x}-1\right)=\left(\sqrt{x}-1\right)^2\left(\sqrt{x}+1\right)\)
\(a,=\dfrac{\left(9-4\sqrt{5}\right)\left(5+2\sqrt{5}\right)}{4}+\dfrac{2\sqrt{5}}{5}\\ =\dfrac{5-2\sqrt{5}}{4}+\dfrac{2\sqrt{5}}{5}\\ =\dfrac{25-10\sqrt{5}+8\sqrt{5}}{20}=\dfrac{25-2\sqrt{5}}{20}\\ b,=\dfrac{\sqrt{x}+2-4}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}=\dfrac{\sqrt{x}-2}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}=\dfrac{1}{\sqrt{x}+2}\\ c,=\dfrac{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}{\left(\sqrt{x}-1\right)^2}-\dfrac{2}{\sqrt{x}-1}\\ =\dfrac{\sqrt{x}+1-2}{\sqrt{x}-1}=\dfrac{\sqrt{x}-1}{\sqrt{x}-1}=1\\ d,=\dfrac{1}{\sqrt{x}-1}+\dfrac{1}{\sqrt{x}+1}+\dfrac{x+1}{1-x}\)
\(=\dfrac{\sqrt{x}+1+\sqrt{x}-1-x-1}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\\ =\dfrac{2\sqrt{x}-x-1}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\\ =\dfrac{-\left(\sqrt{x}-1\right)^2}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}=\dfrac{-1}{\sqrt{x}+1}\)

b: Xét tứ giác AEHF có
\(\widehat{AEH}+\widehat{AFH}=180^0\)
Do đó: AEHF là tứ giác nội tiếp

a) \(A=\dfrac{\sqrt[]{x}+2}{\sqrt[]{x}-5}\) có nghĩa \(\Leftrightarrow\left\{{}\begin{matrix}x\ge0\\\sqrt[]{x}-5\ne0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\ge0\\\sqrt[]{x}\ne5\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x\ge0\\x\ne25\end{matrix}\right.\)
Khi \(x=16\Rightarrow A=\dfrac{\sqrt[]{16}+2}{\sqrt[]{16}-5}=\dfrac{4+2}{4-5}=-6\)
b) \(B=\dfrac{3}{\sqrt[]{x}+5}+\dfrac{20-2\sqrt[]{x}}{x-25}\)
B có nghĩa \(\Leftrightarrow\left\{{}\begin{matrix}x\ge0\\x-25\ne0\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x\ge0\\x\ne25\end{matrix}\right.\)
\(\Leftrightarrow B=\dfrac{3\left(\sqrt[]{x}-5\right)+20-2\sqrt[]{x}}{\left(\sqrt[]{x}+5\right)\left(\sqrt[]{x}-5\right)}\)
\(\Leftrightarrow B=\dfrac{3\sqrt[]{x}-15+20-2\sqrt[]{x}}{\left(\sqrt[]{x}+5\right)\left(\sqrt[]{x}-5\right)}\)
\(\Leftrightarrow B=\dfrac{\sqrt[]{x}+5}{\left(\sqrt[]{x}+5\right)\left(\sqrt[]{x}-5\right)}\)
\(\Leftrightarrow B=\dfrac{1}{\sqrt[]{x}-5}\left(dpcm\right)\)
c) \(A=\dfrac{\sqrt[]{x}+2}{\sqrt[]{x}-5}\in Z\left(x\in Z\right)\)
\(\Leftrightarrow\sqrt[]{x}+2⋮\sqrt[]{x}-5\)
\(\Leftrightarrow\sqrt[]{x}+2-\left(\sqrt[]{x}-5\right)⋮\sqrt[]{x}-5\)
\(\Leftrightarrow\sqrt[]{x}+2-\sqrt[]{x}+5⋮\sqrt[]{x}-5\)
\(\Leftrightarrow7⋮\sqrt[]{x}-5\)
\(\Leftrightarrow\sqrt[]{x}-5\in U\left(7\right)=\left\{-1;1;-7;7\right\}\)
\(\Leftrightarrow x\in\left\{16;36;144\right\}\)
d) \(A>B\left(2\sqrt[]{x}+5\right)\)
\(\Leftrightarrow\dfrac{\sqrt[]{x}+2}{\sqrt[]{x}-5}>\dfrac{1}{\sqrt[]{x}-5}\left(2\sqrt[]{x}+5\right)\)
\(\Leftrightarrow\sqrt[]{x}+2>2\sqrt[]{x}+5\)
\(\Leftrightarrow\sqrt[]{x}< -3\)
mà \(\sqrt[]{x}\ge0\)
\(\Leftrightarrow x\in\varnothing\)









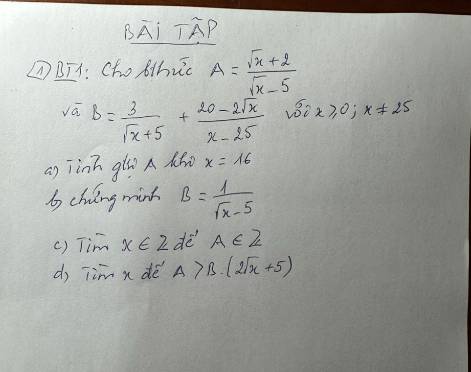

 ai giúp mình giải với mình cần câu c với câu d thôi cũng đc ạ! cảm ơn
ai giúp mình giải với mình cần câu c với câu d thôi cũng đc ạ! cảm ơn
Bài 3:
\(a,m=-2\Leftrightarrow y=-3x-3\\ b,\Leftrightarrow\left\{{}\begin{matrix}m-1=2\\2m+1\ne1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m=3\\m\ne0\end{matrix}\right.\Leftrightarrow m=3\\ c,\text{PT hoành độ giao điểm: }2x-7=\left(m-1\right)x+2m+1\\ \text{Thay }x=2\\ \Leftrightarrow2m-2+2m+1=-3\\ \Leftrightarrow4m=-2\Leftrightarrow m=-\dfrac{1}{2}\\ d,\text{Gọi điểm cần tìm là }A\left(x_0;y_0\right)\\ \Leftrightarrow y_0=\left(m-1\right)x_0+2m+1\\ \Leftrightarrow mx_0-x_0+2m+1-y_0=0\\ \Leftrightarrow m\left(x_0+2\right)+\left(1-x_0-y_0\right)=0\\ \Leftrightarrow\left\{{}\begin{matrix}x_0+2=0\\1-x_0-y_0=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x_0=-2\\y_0=3\end{matrix}\right.\Leftrightarrow A\left(-2;3\right)\)