
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



1) \(x^3+y^3+z^3-3xyz=\left(x^3+3x^2y+3xy^2+y^3\right)+z^3-3xyz-3x^2y-3xy^2=\left(x+y\right)^3+z^3-3xy\left(x+y+z\right)=\left(x+y+z\right)\left[\left(x+y\right)^2-\left(x+y\right)z+z^2\right]-3xy\left(x+y+z\right)=\left(x+y+z\right)\left(x^2+2xy+y^2-xz-yz+z^2\right)-3xy\left(x+y+z\right)=\left(x+y+z\right)\left(x^2+2xy+y^2-xz-yz+z^2-3xy\right)=\left(x+y+z\right)\left(x^2+y^2+z^2-xy-xz-yz\right)\)
2) Ta có: \(\left(a+b+c\right)^2=a^2+b^2+c^2\)
\(\Leftrightarrow a^2+b^2+c^2+2\left(ab+bc+ac\right)=a^2+b^2+c^2\)
\(\Leftrightarrow ab+bc+ac=0\)
\(\dfrac{1}{a^3}+\dfrac{1}{b^3}+\dfrac{1}{c^3}=\dfrac{3}{abc}\)
\(\Leftrightarrow\dfrac{a^3b^3+b^3c^3+a^3c^3}{a^3b^3c^3}=\dfrac{3}{abc}\)
\(\Leftrightarrow\dfrac{a^3b^3+b^3c^3+a^3c^3}{a^2b^2c^2}=3\)
\(\Leftrightarrow a^3b^3+b^3c^3+a^3c^3=3a^2b^3c^2\)
\(\Leftrightarrow\left(ab+bc\right)^3-3ab^2c\left(ab+bc\right)+a^3b^3-3a^2b^2c^2=0\)
\(\Leftrightarrow\left(ab+bc+ac\right)\left[\left(ab+bc\right)^2-\left(ab+bc\right)ac+a^2c^2\right]-3ab^2c\left(ab+bc+ac\right)=0\)
\(\Leftrightarrow0+0=0\left(đúng\right)\)

\(1,7x-8=4x+7\)
\(\Leftrightarrow7x-8-4x=7\)
\(\Leftrightarrow7x-4x=7+8\)
\(\Leftrightarrow3x=15\)
\(\Rightarrow x=5\)
\(2,3-2x=3\left(x+1\right)-x-2\)
\(\Leftrightarrow3-2x=2x+1\)
\(\Leftrightarrow-2x+3=2x+1\)
\(\Leftrightarrow-2x-2x=1-3\)
\(\Leftrightarrow-4x=-2\)
\(\Rightarrow x=\dfrac{1}{2}\)
\(3,5\left(3x+2\right)=4x+1\)
\(\Leftrightarrow5.3x+5.2=4x+1\)
\(\Leftrightarrow15x+10=4x+1\)
\(\Leftrightarrow15x-4x=1-10\)
\(\Leftrightarrow11x=-9\)
\(\Rightarrow x=\dfrac{-9}{11}\)

a: Xét tứ giác MIPC có
K là trung điểm của MP
K là trung điểm của IC
Do đó: MIPC là hình bình hành
mà MI=PI
nên MIPC là hình thoi

a: Xét ΔHAC vuông tại H và ΔABC vuông tại A có
\(\widehat{C}\) chung
Do đó: ΔHAC~ΔABC
b: ΔABC vuông tại A
=>\(AB^2+AC^2=BC^2\)
=>\(BC^2=15^2+20^2=625\)
=>BC=25
Xét ΔABC vuông tại A có AH là đường cao
nên \(\left\{{}\begin{matrix}BH\cdot BC=BA^2\\AH\cdot BC=AB\cdot AC\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}BH\cdot25=15^2=225\\AH\cdot25=15\cdot20=300\end{matrix}\right.\)
=>BH=9; AH=12

a: \(M=\dfrac{5x+5-8-4x+4}{\left(x-1\right)\left(x+1\right)}=\dfrac{x+1}{\left(x-1\right)\left(x+1\right)}=\dfrac{1}{x-1}\)
b: \(N=\dfrac{5x+5-8-4x+4}{\left(x-1\right)\left(x+1\right)}=\dfrac{x+1}{\left(x-1\right)\left(x+1\right)}=\dfrac{1}{x-1}\)
1. \(M=\dfrac{5}{x-1}-\dfrac{8}{x^2-1}-\dfrac{4}{x+1}\left(x\ne\pm1\right).\)
\(M=\dfrac{5\left(x+1\right)-8-4\left(x-1\right)}{\left(x-1\right)\left(x+1\right)}\)\(M=\dfrac{5x+5-8-4x+4}{\left(x-1\right)\left(x+1\right)}=\dfrac{x+1}{\left(x-1\right)\left(x+1\right)}\)
\(M=\dfrac{1}{x-1}.\)
2. \(N=\dfrac{5}{x-1}+\dfrac{8}{1-x^2}-\dfrac{4}{x+1}\left(x\ne\pm1\right).\)
\(N=\dfrac{5\left(x+1\right)-8-4\left(x-1\right)}{\left(x-1\right)\left(x+1\right)}=\dfrac{5x+5-8-4x+4}{\left(x-1\right)\left(x+1\right)}\)
\(N=\dfrac{x+1}{\left(x-1\right)\left(x+1\right)}=\dfrac{1}{x-1}.\)
3. \(Q=\dfrac{1}{2x-1}-\dfrac{4}{4x^2-1}-\dfrac{2}{2x+1}\left(x\ne\pm\dfrac{1}{2}\right).\)
\(Q=\dfrac{2x+1-4-2\left(2x-1\right)}{\left(2x-1\right)\left(2x+1\right)}=\dfrac{2x-3-4x+2}{\left(2x-1\right)\left(2x+1\right)}\)
\(Q=\dfrac{-2x-1}{\left(2x-1\right)\left(2x+1\right)}=\dfrac{-1}{2x-1}.\)
4. \(F=\dfrac{x+3}{x-2}+\dfrac{x+2}{3-x}+\dfrac{x+2}{x^2-5x+6}\left(x\ne2,x\ne3\right).\)
\(F=\dfrac{x+3}{x-2}-\dfrac{x+2}{x-3}+\dfrac{x+2}{\left(x-3\right)\left(x-2\right)}\)
\(F=\dfrac{\left(x+3\right)\left(x-3\right)-\left(x+2\right)\left(x-2\right)+x+2}{\left(x-2\right)\left(x-3\right)}\)
\(F=\dfrac{x^2-9-x^2+4+x+2}{\left(x-2\right)\left(x-3\right)}=\dfrac{x-3}{\left(x-2\right)\left(x-3\right)}\)
\(F=\dfrac{1}{x-2}.\)

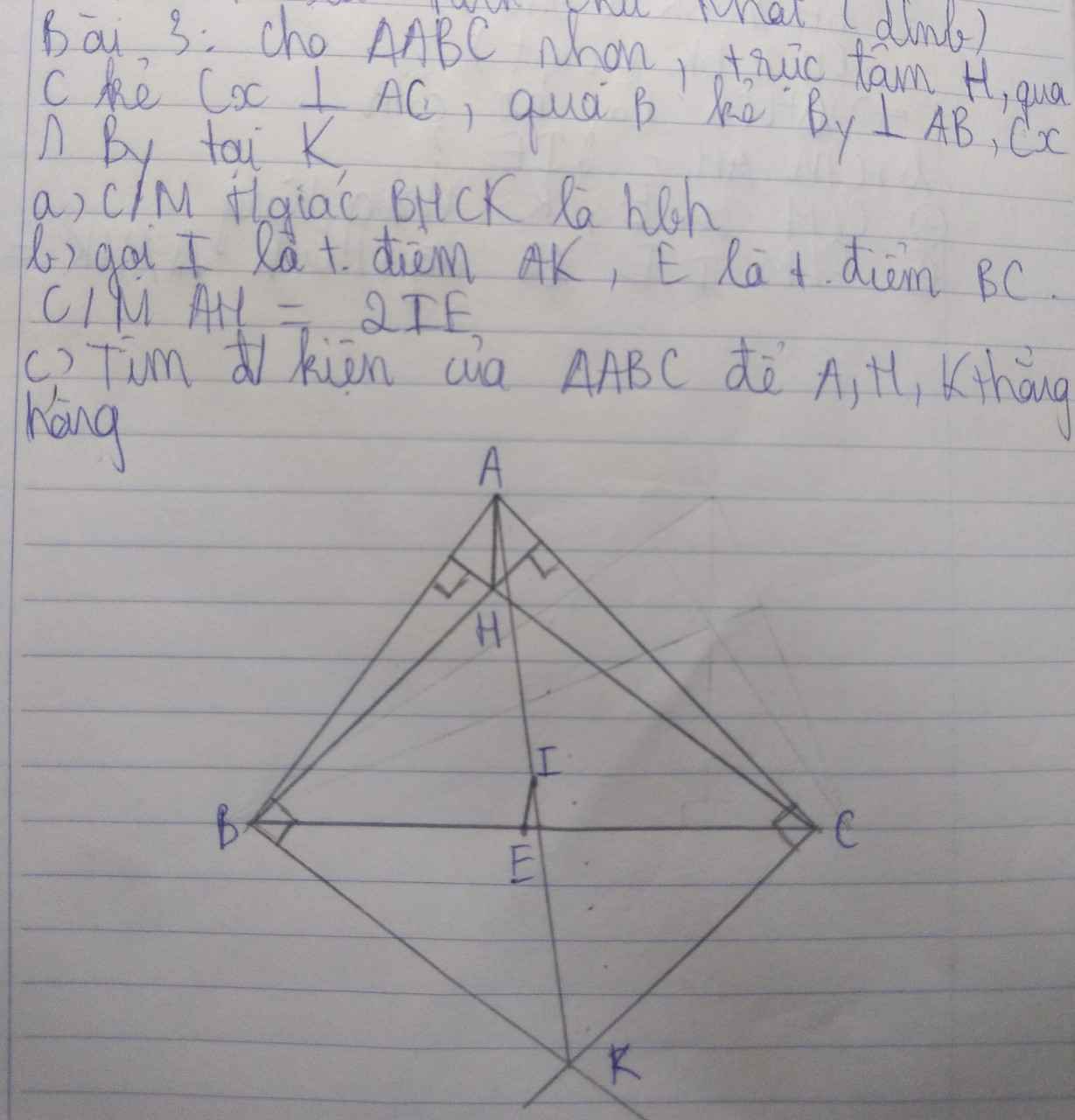
a: Xét tứ giác BHCK có
BK//CH
BH//CK
Do đó:BHCK là hình bình hành

a: góc AEH=góc ADH=góc DAE=90 độ
=>AEHD là hcn
b: XétΔAEH vuông tại E và ΔAHC vuông tại H có
góc EAH chung
=>ΔAEH đồng dạng với ΔAHC
c: ΔAHC vuông tại H có HE là đường cao
nên HE^2=AE*EC

a: =>8x-3=4 hoặc 8x-3=-4
=>8x=7 hoặc 8x=-1
=>x=7/8 hoặc x=-1/8
b: =>6x-5=5x-4 hoặc 6x-5=4-5x
=>6x-5x=-4+5 hoặc 6x+5x=4+5
=>x=1 hoặc 11x=9
=>x=1 hoặc x=9/11
c: \(\Leftrightarrow\left\{{}\begin{matrix}-5x+9>=0\\\left(-5x+9\right)^2-\left(x-6\right)^2=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}-5x>=-9\\\left(5x-9-x+6\right)\left(5x-9+x-6\right)=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x< =\dfrac{9}{5}\\\left(4x-3\right)\left(6x-15\right)=0\end{matrix}\right.\Leftrightarrow x=\dfrac{3}{4}\)
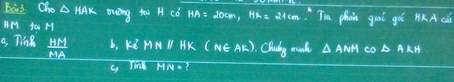






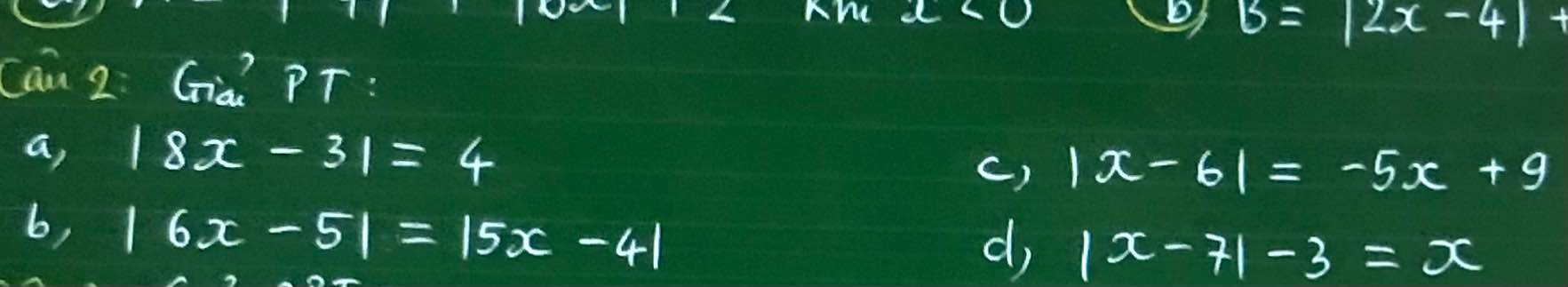
ê bây nha học thầy thanh lên dây ak:))
:)))) wtf đứa nào v