Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Xét ΔABC có
AM vừa là đường phân giác, vừa là đường trung tuyến
nên ΔABC cân tại A

Vì Δ A B C cân tại A có AM là đường trung tuyến nên AM cũng là đường cao, đường trung trực và đường phân giác của tam giác ABC
Chọn đáp án D

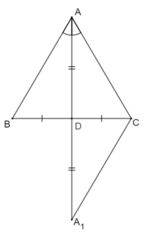
- Giả sử AD vừa là đường trung tuyến, vừa là đường phân giác của tam giác ABC.
Ta cần chứng minh ∆ABC cân tại A.
Kéo dài AD một đoạn DA1 sao cho DA1 = AD.
- ∆ADB và ∆A1DC có
AD = DA1 (cách vẽ)
BD = CD (do D là trung điểm BC)

⇒ ∆ADB = ∆A1DC (c.g.c)
⇒ 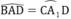 (hai góc tương ứng), AB = A1C (hai cạnh tương ứng) (1)
(hai góc tương ứng), AB = A1C (hai cạnh tương ứng) (1)
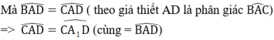
⇒ ∆ACA1 cân tại C ⇒ AC = A1C (2)
Từ (1) và (2) ⇒ AB = AC.
Vậy ∆ABC cân tại A
Tức là: Nếu tam giác có một đường trung tuyến đồng thời là đường phân giác thì tam giác đó là một tam giác cân.

Xét tam giác ABC có AM là đường cao đồng thời là đường trung tuyến
\(\Rightarrow\Delta ABC\) cân tại A

sửa đề tam giác DEF là tam giác gì ?
Vì tam giác DEF có DM là đường trung tuyến
đồng thời là đường phân giác
nên tam giác DEF cân tại D


Cm: a) Xét t/giác ABM và t/giác ACM
có AM : chung
góc AMB = góc AMC = 900 (gt)
BM = CM (gt)
=> t/giác ABM = t/giác ACM (c.g.c)
=> AB = AC (hai cạnh tương ứng)
=> t/giác ABC cân tạiA
Ta có AM là đường trung tuyến vậy suy ra MB = MC
Xét ⚠️ BAM và ⚠️ CAM có:
MB = MC( Cmt)
Góc AMC=Góc AMB=90 độ
AM cạnh chung
Suy ra ⚠️ BAM = ⚠️ CAM( c-g-c )
suy ra AB =AC (vì ⚠️ BAM = ⚠️ CAM)
suy ra ⚠️ ABC cân tại A