Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Đáp án C
2 C 14 k + 1 = C 14 k + C 14 k + 2 ⇔ 2. 14 ! ( k + 1 ) ! ( 13 − k ) ! = 14 ! ( 14 − k ) ! k ! + 14 ! ( 12 − k ) ! ( k + 2 ) ! 14 ! k ! ( 12 − k ) ! ( 2 ( 13 − k ) ( k + 1 ) − 1 ( 14 − k ) ( 13 − k ) − 1 ( k + 2 ) ( k + 1 ) ) = 0 ⇔ − 4 k 2 + 48 k − 128 = 0 ⇔ k = 8 k = 4
Đáp án C
2 C 14 k + 1 = C 14 k + C 14 k + 2 ⇔ 2 . 14 ! ( k + 1 ) ! 13 - k ! = 14 ! 14 - k ! k ! + 14 ! ( k + 2 ) ! 12 - k ! 14 ! k ! 12 - k ! 2 13 - k k + 1 - 1 14 - k 13 - k - 1 k + 2 k + 1 = 0 ⇔ - 4 k 2 + 48 k - 128 = 0 ⇔ [ k = 8 k = 4
Đáp án D
Phương pháp:
Sử dụng công thức tổng quát của CSC 
và tính chất của CSN 
Cách giải:
a, b, c lần lượt là số thứ nhất, thứ tư và thứ tám của một cấp số cộng công sai là s ≠ 0
nên ta có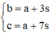 
a, b, c theo thứ tự tạo thành một cấp số nhân với công bội khác 1 nên ta có
Chọn đáp án B
Phương pháp
Chia các TH sau:
TH1: a<b<c.
TH2: a=b<c.
TH3: a<b=c.
TH4: a=b=c.
Cách giải
Gọi số tự nhiên có 3 chữ số là a b c ¯ (0≤a,b,c≤9, a≠0).
=> S có 9.10.10=900 phần tử. Chọn ngẫu nhiên một số từ S => n(Ω)=900
Gọi A là biến cố: “Số được chọn thỏa mãn a≤b≤c”.
TH1: a<b<c. Chọn 3 số trong 9 số từ 1 đến 9, có duy nhất một cách xếp chúng theo thứ tự tăng dần từ trái qua phải nên TH này có C 9 3 số thỏa mãn.
TH2: a=b<c, có C 9 2 số thỏa mãn.
TH3: a<b=c có C 9 2 số thỏa mãn.
TH4: a=b=c có 9 số thỏa mãn.
⇒ n ( A ) = C 9 3 + 2 C 9 2 + 9 = 165
Vậy P ( A ) = 11 60 .
