Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn D.
Phương pháp: Ta có thể sử dụng phương pháp loại trừ.
Cách giải: Ta thấy hình chóp ngũ giác thỏa mãn giả thiết nhưng không thỏa mãn các phương án A, B, C. Nên phương án D phù hợp.

Chọn D
Gọi tổng số các mặt của (H) là m và tổng số các cạnh của (H) là c.
Ta có: 2 ( p 1 + p 2 + … + p m ) + m = 2 c . Trong đó mỗi mặt nào đó có số cạnh là 2 p i + 1 , i = 1 , … , m
Do đó m chia hết cho 2. Hơn nữa có ít nhất một mặt ngũ giác nên tổng số mặt lớn hơn 5, do đó, tổng số cạnh lớn hơn 9 và tổng số đỉnh lớn hơn 5.
Hình chóp có đáy là ngũ giác của tổng số mặt là một số chẵn.

Phương pháp:
Sử dụng lý thuyết khối đa diện để làm bài toán.
Cách giải:
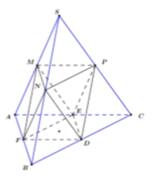
Khối đa diện được tạo từ 6 đỉnh là 6 trung điểm của các cạnh của tứ diện đều là khối bát diện đều có 6 đỉnh, 12 cạnh và 8 mặt.
Khối bát diện đều là khối đa diện có 9 mặt đối xứng.
Chọn: D

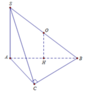
Đáp án D
Vì B C ⊥ S A B C ⊥ C A ⇒ B C ⊥ S A C ⇒ B C ⊥ S C ⇒ O là tâm đường tròn ngoại tiếp tam giác SBC
Vì S A ⊥ A B C ⇒ H là trung điểm của AB
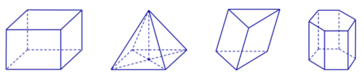

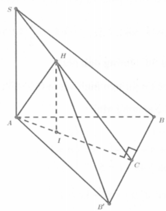
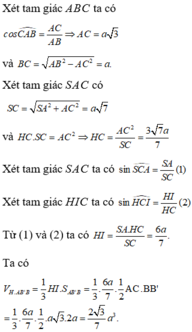
Đáp án B
Luôn tồn tại một hình đa diện H có 4 mặt phẳng đối xứng và có đúng 5 đỉnh, H không có tâm đối xứng