Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Có 150g dung dịch chứa 40g muối. Ta phải pha thêm bao nhiêu nước nữa để dung dịch có tỉ lệ 20% muối.


Gọi khối lượng muối trong dung dịch ban đầu là x, khối lượng dung dịch ban đầu là m, ta có:
\(\dfrac{x}{m}=\dfrac{10}{100}=\dfrac{1}{10}\Rightarrow m=10x\) (1)
Sau khi pha thêm 200g nước:
\(\dfrac{x}{m+200}=\dfrac{6}{100}=\dfrac{3}{50}\) (2)
Thế (1) vào (2):
\(\dfrac{x}{10x+200}=\dfrac{3}{50}\Rightarrow20x=600\Rightarrow x=30\) (g)

Gọi trọng lượng nước trong dung dịch trước khi đổ thêm nước là: x (g) (x > 0)

Vậy trước khi đổ thêm nước, trong dung dịch có 160g nước.
Kiến thức áp dụng
Để giải bài toán bằng cách lập phương trình ta làm theo các bước:
Bước 1: Lập phương trình
+ Chọn ẩn và đặt điều kiện cho ẩn
+ Biểu diễn tất cả các đại lượng khác qua ẩn vừa chọn.
+ Lập phương trình biểu thị mối quan hệ giữa các đại lượng.
Bước 2: Giải phương trình
Bước 3: Đối chiếu điều kiện rồi kết luận.

Gọi trọng lượng nước trong dung dịch trước khi đổ thêm nước là: x (g) (x > 0)
Nồng độ muối của dung dịch khi đó là: 40 x + 40
Đổ thêm 200g nước vào dung dịch thì trọng lượng của dung dịch sẽ là: x+40+200(g)
Nồng độ của dung dịch bây giờ là: 40 x + 240
Vì nồng độ muối giảm 10% nên ta có có phương trình: 40 x + 40 - 40 x + 240 = 10 100
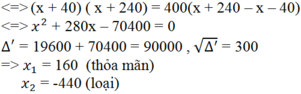
Vậy trước khi đổ thêm nước, trong dung dịch có 160g nước.
Lời giải:
Lượng muối trong dung dịch ban đầu:
$300.0,15=45$ (g)
Để dung dịch chứa 10% muối thì dung dịch có khối lượng là:
$45:0,1=450$ (g)
Lượng nước cần thêm: $450-300=150$ (g)