Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) y = x 3 − (m + 4) x 2 − 4x + m
⇔ ( x 2 − 1)m + y − x 3 + 4 x 2 + 4x = 0
Đồ thị của hàm số (1) luôn luôn đi qua điểm A(x; y) với mọi m khi (x; y) là nghiệm của hệ phương trình:
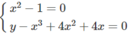
Giải hệ, ta được hai nghiệm:
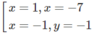
Vậy đồ thị của hàm số luôn luôn đi qua hai điểm (1; -7) và (-1; -1).
b) y′ = 3 x 2 − 2(m + 4)x – 4
Δ′ = ( m + 4 ) 2 + 12
Vì Δ’ > 0 với mọi m nên y’ = 0 luôn luôn có hai nghiệm phân biệt (và đổi dấu khi qua hai nghiệm đó). Từ đó suy ra đồ thị của (1) luôn luôn có cực trị.
c) Học sinh tự giải.
d) Với m = 0 ta có: y = x 3 – 4 x 2 – 4x.
Đường thẳng y = kx sẽ cắt (C) tại ba điểm phân biệt nếu phương trình sau có ba nghiệm phân biệt: x 3 – 4 x 2 – 4x = kx.
Hay phương trình x 2 – 4x – (4 + k) = 0 có hai nghiệm phân biệt khác 0, tức là:
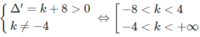

Đáp án B
Gọi ![]() là điểm cố định cần tìm.
là điểm cố định cần tìm.
Ta có ![]()
![]()
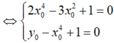

hoặc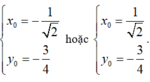
Vậy đồ thị hàm số đã cho đi qua bốn điểm cố định.

Đáp án C
Gọi ![]() là điểm cố định cần tìm.
là điểm cố định cần tìm.
Ta có: ![]()
![]()
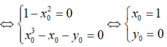
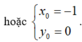 .
.
Vậy đồ thị hàm số đã cho đi qua hai điểm cố định.
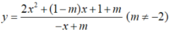 luôn luôn đi qua một điểm M
M
(
x
m
;
y
m
)
cố định khi m thay đổi, khi đó
x
m
+
y
m
bằng
luôn luôn đi qua một điểm M
M
(
x
m
;
y
m
)
cố định khi m thay đổi, khi đó
x
m
+
y
m
bằng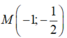
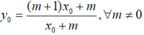
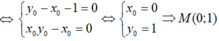
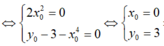
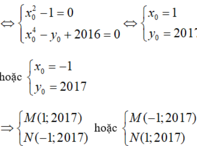
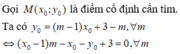
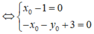
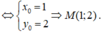
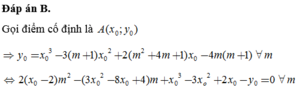
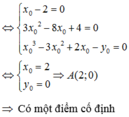
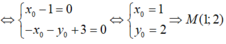
Đáp án C
Gọi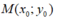 là điểm cố định cần tìm.
là điểm cố định cần tìm.
Ta có