Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Để A có giá trị nguyên => n - 5 chia hết n + 1
=> n + 1 - 6 chia hết n + 1
Vì n + 1 chia hết n + 1
=> 6 chia hết n + 1
=> n + 1 thuộc Ư(6) = {........}
=> .......................Còn lại bạn tự làm nha!
b) Giả sử tử và mẫu cùng chia hết cho số nguyên tố d
=> n - 5 chia hết d và n + 1 chia hết d
=> ( n+1) - ( n - 5) chia hết d
=> 6 chia hết d => d = 2 ; 3 ( vì d là số nguyên tố)
=> Có 2 trường hợp .....tự làm nha
a,n-5/n-1=((n-1)-4)/n-1
=1-(4/n-1)
=> n-1 thuộc Ư(4) =>n-1 =1, -1, 2, -2, 4, -4
=>.......

Xét bài toán phụ sau:
Nếu \(a+b+c=0\Leftrightarrow\sqrt{\frac{1}{a^2}+\frac{1}{b^2}+\frac{1}{c^2}}=\left|\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\right|\) \(\left(a,b,c\ne0\right)\)
Thật vậy
Ta có: \(\sqrt{\frac{1}{a^2}+\frac{1}{b^2}+\frac{1}{c^2}}=\sqrt{\left(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\right)^2-2\left(\frac{1}{ab}+\frac{1}{bc}+\frac{1}{ca}\right)}\)
\(=\sqrt{\left(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\right)^2-2\cdot\frac{a+b+c}{abc}}=\sqrt{\left(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\right)^2-2\cdot\frac{0}{abc}}\)
\(=\sqrt{\left(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\right)^2}=\left|\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\right|\)
Bài toán được chứng minh
Quay trở lại, ta sẽ áp dụng bài toán phụ vào bài chính:
Ta có: \(P=\sqrt{\frac{1}{2^2}+\frac{1}{1^2}+\frac{1}{3^2}}+\sqrt{\frac{1}{2^2}+\frac{1}{3^2}+\frac{1}{5^2}}+...+\sqrt{\frac{1}{2^2}+\frac{1}{779^2}+\frac{1}{801^2}}\)
Vì \(2+1+\left(-3\right)=0\) nên:
\(\sqrt{\frac{1}{2^2}+\frac{1}{1^2}+\frac{1}{3^2}}=\sqrt{\frac{1}{2^2}+\frac{1}{1^2}+\frac{1}{\left(-3\right)^2}}=\sqrt{\left(\frac{1}{2}+\frac{1}{1}-\frac{1}{3}\right)^2}=\frac{1}{2}+1-\frac{1}{3}\)
Tương tự ta tính được:
\(\sqrt{\frac{1}{2^2}+\frac{1}{3^2}+\frac{1}{5^2}}=\frac{1}{2}+\frac{1}{3}-\frac{1}{5}\) ; ... ; \(\sqrt{\frac{1}{2^2}+\frac{1}{799^2}+\frac{1}{801^2}}=\frac{1}{2}+\frac{1}{799}-\frac{1}{801}\)
\(\Rightarrow P=\frac{1}{2}+1-\frac{1}{3}+\frac{1}{2}+\frac{1}{3}-\frac{1}{5}+...+\frac{1}{2}+\frac{1}{799}-\frac{1}{801}\)
\(=\frac{1}{2}\cdot400+\left(1-\frac{1}{3}+\frac{1}{3}-\frac{1}{5}+...+\frac{1}{799}-\frac{1}{801}\right)\)
\(=200+\frac{800}{801}=\frac{161000}{801}=\frac{a}{b}\Rightarrow\hept{\begin{cases}a=161000\\b=801\end{cases}}\)
\(\Rightarrow Q=161000-801\cdot200=800\)

\(\sqrt{\dfrac{1}{4}+\dfrac{1}{\left(2n-1\right)^2}+\dfrac{1}{\left(2n+1\right)^2}}=\sqrt{\dfrac{\left(2n-1\right)^2\left(2n+1\right)^2+4\left(2n-1\right)^2+4\left(2n+1\right)^2}{4\left(2n-1\right)^2\left(2n+1\right)^2}}\)
\(=\sqrt{\dfrac{\left(4n^2-1\right)^2+4\left(4n^2-4n+1\right)+4\left(4n^2+4n+1\right)}{4\left(2n-1\right)^2\left(2n+1\right)^2}}\)
\(=\sqrt{\dfrac{16n^4+24n^2+9}{4\left(2n-1\right)^2\left(2n+1\right)^2}}=\sqrt{\dfrac{\left(4n^2+3\right)^2}{4\left(2n-1\right)^2\left(2n+1\right)^2}}=\dfrac{4n^2+3}{2\left(2n-1\right)\left(2n+1\right)}\)
\(=\dfrac{\left(4n^2-1\right)+4}{2\left(2n-1\right)\left(2n+1\right)}=\dfrac{1}{2}+\dfrac{2}{\left(2n-1\right)\left(2n+1\right)}\)
\(=\dfrac{1}{2}+\dfrac{1}{2n-1}-\dfrac{1}{2n+1}\)
Do đó:
\(P=\left(\dfrac{1}{2}+\dfrac{1}{1}-\dfrac{1}{3}\right)+\left(\dfrac{1}{2}+\dfrac{1}{3}-\dfrac{1}{5}\right)+...+\left(\dfrac{1}{2}-\dfrac{1}{399}-\dfrac{1}{401}\right)\)
\(=\dfrac{1}{2}.200+1-\dfrac{1}{401}=\dfrac{40500}{401}\)
\(\Rightarrow Q=400\)


gọi d=( n+1, 2n+1)
=> n+1 chia hết cho d=> 2n+2 chia hết cho d
=>2n+1 chia hết cho d=> 2n+1 chia hết cho d
=> ( 2n+2)-( 2n+1) chia hết cho d
=> 1 chia hết cho d
=> d= -1 hoặc +1
=> phân số n+1/2n+1 là phân số tối giản
b, giải
Gọi d là \(UCLN\left(n+1,n+2\right)\)
\(\Rightarrow\orbr{\begin{cases}n+1⋮d\\n+2⋮d\end{cases}}\)
\(\Rightarrow\left(n+1\right)-\left(n+2\right)⋮d\)
\(\Rightarrow1⋮d\)
\(\Rightarrow d=1\)
\(\Rightarrow UCLN\left(n+1,n+2\right)=1\)
\(\Rightarrow\frac{n+1}{n+2}\) là phân số tối giản (ĐPCM)

a/
\(VT\ge\frac{\frac{1}{2}\left(a+b\right)^2}{a+b}+\frac{\frac{1}{2}\left(b+c\right)^2}{b+c}+\frac{\frac{1}{2}\left(c+a\right)^2}{c+a}=a+b+c\ge3\sqrt[3]{abc}=3\)
Dấu "=" xảy ra khi \(a=b=c=1\)
b/ Ta có: \(x^4+y^4\ge\frac{1}{2}\left(x^2+y^2\right)\left(y^2+y^2\right)\ge xy\left(x^2+y^2\right)\)
\(\Rightarrow VT\le\frac{1}{a+bc\left(b^2+c^2\right)}+\frac{1}{b+ca\left(a^2+c^2\right)}+\frac{1}{c+ab\left(a^2+b^2\right)}\)
\(VT\le\frac{1}{a+\frac{1}{a}\left(b^2+c^2\right)}+\frac{1}{b+\frac{1}{b}\left(a^2+c^2\right)}+\frac{1}{c+\frac{1}{c}\left(a^2+b^2\right)}\)
\(VT\le\frac{a}{a^2+b^2+c^2}+\frac{b}{a^2+b^2+c^2}+\frac{c}{a^2+b^2+c^2}=\frac{a+b+c}{a^2+b^2+c^2}\)
\(VT\le\frac{a+b+c}{\frac{1}{3}\left(a+b+c\right)^2}=\frac{3}{a+b+c}\le\frac{3}{3\sqrt[3]{abc}}=1\)
Dấu "=" xảy ra khi \(a=b=c=1\)

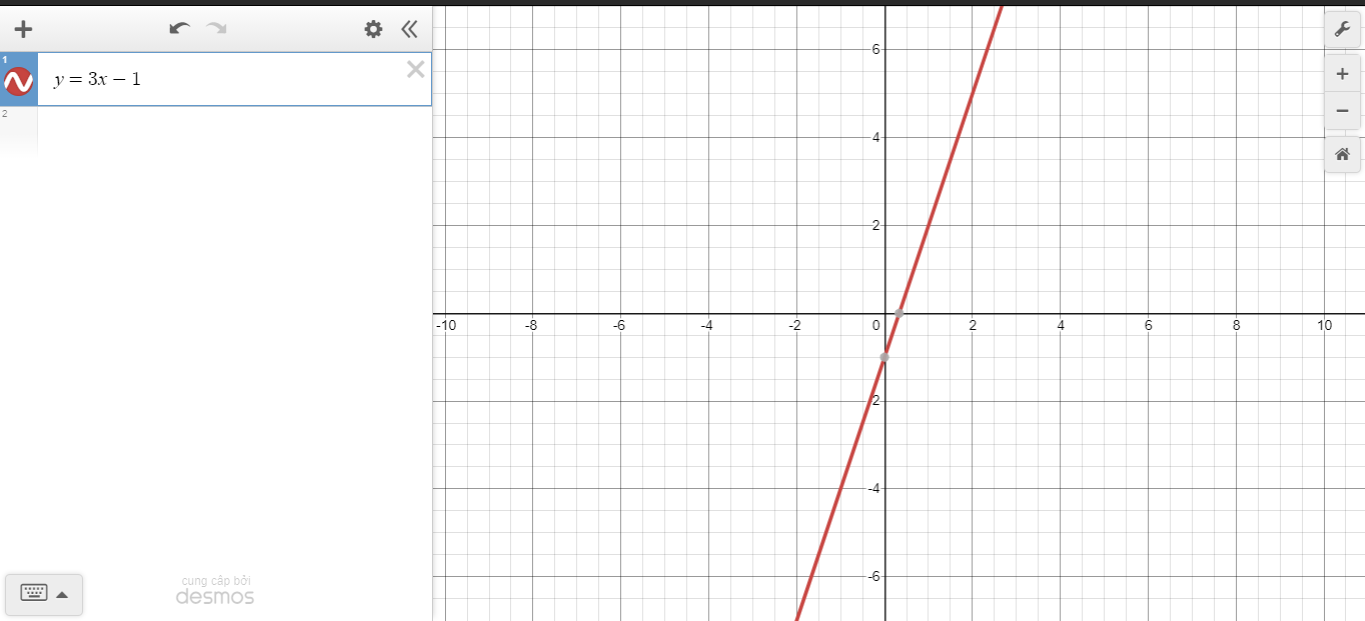
\(a,\) \(\left(d\right)\) đi qua \(A\left(1;2\right)\Leftrightarrow x=1;y=2\)
\(\Leftrightarrow2=m+1-2m+3\Leftrightarrow m=2\)
\(b,m=2\Leftrightarrow\left(d\right):y=3x-2\cdot2+3=3x-1\)
\(y=2\Leftrightarrow x=1\Leftrightarrow A\left(1;2\right)\\ y=5\Leftrightarrow x=2\Leftrightarrow B\left(2;5\right)\)

1+(-1/2)+1/4+(-1/8)+...+(-1/2)^N-1+....=a/b. tìm a+b. biết a/b là phân số tối giản