Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A.
* Hướng dẫn giải:
Dễ thấy AB = BC và A B C ⏜ = 60 o nên tam giác ABC đều.
Gọi H là hình chiếu của A lên (ABCD).
Do SA = SB =SC nên H là tâm đường tròn ngoại tiếp tam giác ABC.
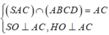
![]()
Mặt khác, H O = 1 3 B O = 1 3 . a 3 2 = a 3 6
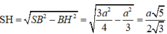
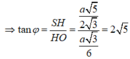

a) Tính \(V_{S.ABM}\)
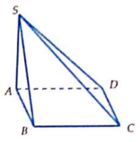
Tam giác ABC cân tại A , SBC cân tại S \(\Rightarrow AM\perp BC;SM\perp BC\) tại M
Vì mp(SBC) vuông góc với mặt đáy suy ra SM vuông góc với mặt đáy
Góc giữa SB và mặt đáy là góc SBM=300
\(\Rightarrow SM=BMtan.\widehat{SBM}=\frac{a}{2}.tan30^0=\frac{a}{2\sqrt{3}}\)
\(\Rightarrow V_{S.ABM}=\frac{1}{3}.SM.S_{ABM}=\frac{1}{3}.\frac{a}{2\sqrt{3}}.\frac{1}{2}.\frac{a}{2}.\frac{a\sqrt{3}}{2}=\frac{a^3}{48}\)
b) Tính k/c SB và AM
Kẻ MH vuông góc với SB tại H
Dễ dàng chứng minh MH là đoạn vuông góc chung giữa SB và AM
Vậy khảong cách giữa SB và AM bằng đoạn MH và bằng \(\frac{BM}{cos.\widehat{HBM}}=\frac{\frac{a}{2}}{cos30^0}=\frac{a}{\sqrt{3}}\)

Chọn D.
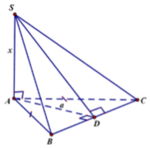
Đặt SA = x > 0. Ta có ![]() Ta có:
Ta có:
![]()
![]()
Xét tam giác vuông SBD, ta có ![]()
Khi đó: ![]()
Vậy ![]()

Gọi O là giao điểm của AC và BD. Dễ thấy \(\Delta OAB\) vuông tại O và \(OB=\dfrac{a\sqrt{3}}{2}\). Từ đó \(OA=\sqrt{AB^2-OB^2}=\sqrt{\left(\dfrac{\sqrt{3}}{2}a\right)^2-a^2}=\sqrt{\dfrac{1}{4}a^2}=\dfrac{a}{2}\) \(\Rightarrow AC=a\).
Vì \(SA\perp mp\left(ABCD\right)\) nên \(SA\perp AC\) tại A hay \(\Delta SAC\) vuông tại A.
Lại có \(\tan SAC=\dfrac{SA}{AC}=\dfrac{a\sqrt{3}}{a}=\sqrt{3}\) nên \(\widehat{SAC}=60^o\), suy ra góc giữa SC và mp(ABCD) bằng 60o \(\Rightarrow\) Chọn A
Chỗ \(\widehat{SAC}\) em sửa lại là \(\widehat{SCA}\) mới đúng ạ.

Đáp án B
Hướng dẫn giải:
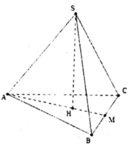
Gọi H là trọng tâm tam giác đều ABC ⇒ S H ⊥ ( A B C )
Gọi M là trung điểm của BC.
Ta có: A H = S A . cos 60 o = a 2
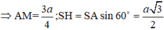
Đặt AB = x
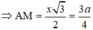
⇒ x = a 3 2
Do đó S A B C = x 2 3 4 = 3 a 2 3 16
⇒ V = 1 3 S H . S A B C = 3 a 2 32
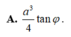
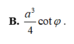

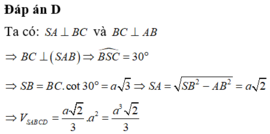
Đáp án D
Phương pháp:
Tính thể tích của khối lăng trụ đứng, có đáy là hình thang cân mà hai cạnh bên bằng đáy bé và bằng 20cm.
Thể tích lớn nhất khi diện tích của hình thang cân lớn nhất.
Cách giải:
Thể tích nước lớn nhất khi diện tích của hình thang cân lớn nhất
Gọi độ dài đường cao là h. Khi đó, AE = BF = h,
Từ đó, suy ra
Bảng xét dấu:
Diện tích hình thang lớn nhất khi h = 10 3