Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

O nằm trên trung trực của MN và PE
=>OM=ON; OP=OE
Xét ΔMOP và ΔNOE có
OM=ON
MP=NE
OP=OE
=>ΔMOP=ΔNOE

\(MN+MP=34\)
\(MN-MP=14\)
\(\Rightarrow2MP=34-14=20\)
\(\Rightarrow MP=10\left(cm\right),MN=34-10=24\left(cm\right)\)
\(Pytago:\)
\(NP=\sqrt{10^2+24^2}=26\left(cm\right)\)
Ta có: \(\left\{{}\begin{matrix}MN+MP=34\\MN-MP=14\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}2MN=48\\MP+MN=34\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}MN=24\\MP=10\end{matrix}\right.\)
Áp dụng định lí Pytago vào ΔMNP vuông tại M, ta được:
\(NP^2=MN^2+MP^2\)
\(\Leftrightarrow NP^2=10^2+24^2=676\)
hay NP=26(cm)
Vậy: MN=10cm; MP=24cm; NP=26cm

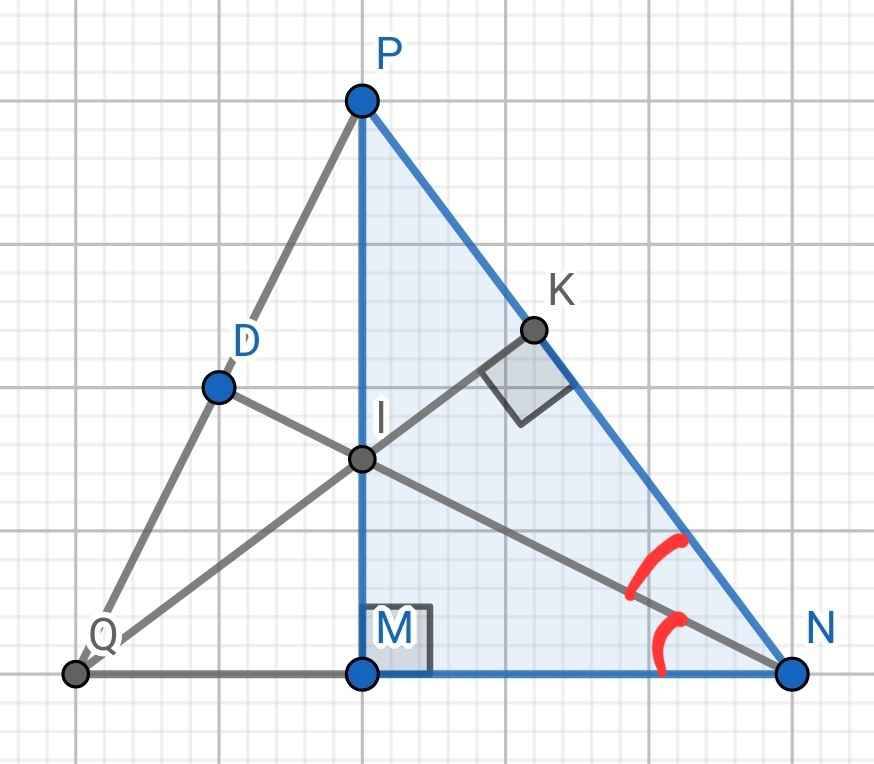
a) Xét hai tam giác vuông: ∆IMN và ∆IKN có:
IN chung
MNI = KNI (do NI là phân giác của ∠MNP)
⇒ ∆IMN = ∆IKN (cạnh huyền - góc nhọn)
b) ∆IKP vuông tại K
IP là cạnh huyền nên IP lớn nhất
IK < IP (1)
Do ∆IMN = ∆IKN (cmt)
⇒ MI = IK (2)
Từ (1) và (2)⇒ MI < IP
c) Xét hai tam giác vuông: ∆IKP và ∆IMQ có:
IM = IK (cmt)
∠PIK = ∠MIQ (đối đỉnh)
∆IKP = ∆IMQ (cạnh góc vuông - góc nhọn kề)
⇒ KP = MQ (hai cạnh tương ứng) (3)
Do ∆IMN = ∆IKN (cmt)
⇒ MN = KN (hai cạnh tương ứng) (4)
Từ (3) và (4) ⇒ KN + KP = MN + MQ
NP = NQ
⇒ ∆NPQ cân tại N
Lại có NI là phân giác của ∠MNP
⇒ NI là phân giác của ∠QNP
⇒ NI cũng là đường cao của ∆NPQ (tính chất tam giác cân)
⇒ ND ⊥ QP

Tự kẻ hình nha
a) - Vì tam giác MNP cân tại M (gt)
=> MN = MP (định nghĩa)
góc MNP = góc MPN (dấu hiệu)
- Vì NH vuông góc với MP (gt)
=> tam giác NHP vuông tại H
- Vì PK vuông góc với MN (gt)
=> tam giác PKN vuông tại K
- Xét tam giác vuông NHP và tam giác vuông PKN, có:
+ Chung NP
+ góc HPN = góc KNP (cmt)
=> tam giác vuông NHP = tam giác vuông PKN (cạnh huyền - góc nhọn)
b) Vì tam giác vuông NHP = tam giác vuông PKN (cmt)
=> góc HNP = góc KPN (2 góc tương ứng)
=> tam giác ENP cân tại E (dấu hiệu)
c) - Vì tam giác ENP cân tại E (cmt)
=> EN = EP (định nghĩa)
- Xét tam giác MNE và tam giác MPE, có:
+ Chung ME
+ MN = MP (cmt)
+ EN = EP (cmt)
=> tam giác MNE = tam giác MPE (ccc)
=> góc NME = góc PME (2 góc tương ứng)
=> ME là đường phân giác góc NMP (tc)

a: Xét ΔKNP vuông tại K và ΔHPN vuong tại H có
PN chung
góc KNP=góc HPN
=>ΔKNP=ΔHPN
b: Xét ΔENP có góc ENP=góc EPN
nên ΔENP cân tại E
c: Xét ΔMNE và ΔMPE có
MN=MP
NE=PE
ME chung
=>ΔMNE=ΔMPE
=>góc NME=góc PME
=>ME là phân giác của góc NMP

góc NMP=180-2*67=180-134=46 độ
góc IMN=46/2=23 độ