Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Đáp án A
Phương pháp giải:
Tìm giá trị lớn nhất của thể tích khối nón và áp dụng công thức tính độ dài cùng tròn
Lời giải:
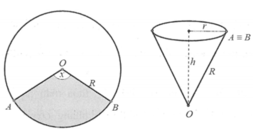
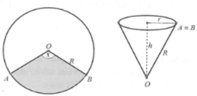
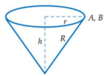
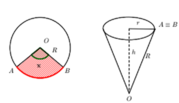
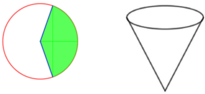
Gọi r, h lần lượt là bán kính đáy, chiều cao của phễu hình nón.
Thể tích của khối nón là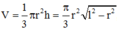 
với l là độ dài đường sinh và l = R bán kính tấm bìa hình tròn => 
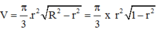vì chuẩn hóa R = 1
Xét hàm số 
trên (0;1) có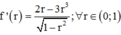 
Ta có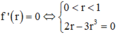 
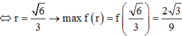
Do đó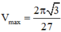 
Dấu “=” xảy ra khi và chỉ khi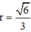 
Mà độ dài cung phần cuộn làm phễu chính là chu vi đáy hình nón
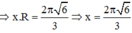
Thể tích cái phễu là V = 1 3 πr 2 h
Ta có chu vi đáy là 2 πr = Rx
Suy ra
r = R x 2 π h = R 2 - r 2 = R 2 - R 2 x 2 4 π 2 = R 2 π 4 π 2 - x 2
Áp dụng bất đẳng thức AM-GM cho 2 số dương ta có:
V = 3 R 3 48 π 2 x 2 . 2 3 π 4 π 2 - x 2 ≤ 3 R 3 2 . 48 π 2 x 2 4 3 π 2 + 4 π 2 - x 2 = 3 R 3 2 . 48 π 2 x 2 16 3 π 2 - x 2 ≤ 1 8 3 R 3 48 π 2 . x 2 + 16 3 π 2 - x 2 2 = 1 8 3 R 3 48 π 2 . 16 2 9 π 4 = 2 3 27 πR 3
Dấu bằng có khi và chỉ khi
2 3 π = 4 π 2 - x 2 x 2 = 16 3 π 2 - x 2 ⇔ x = 2 2 3 π
Vậy 2 3 27 πR 3 khi và chỉ khi x = 2 2 3 πR 3
Đáp án A
Đáp án D
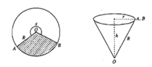
Gọi r;h lần lượt là bán kính đáy và chiều cao của khối nón ⇒ V N = 1 3 π r 2 h
Mà h = l 2 − r 2 = R 2 − r 2 = 81 − r 2 Suy ra V N = 1 3 π r 2 81 − r 2 = π 3 r 4 81 − r 2
Ta có r 2 . r 2 . 162 − 2 r 2 2 ≤ r 2 + r 2 + 162 − 2 r 2 3 2.27 = 78732 ⇒ V ≤ π 3 . 78732 ⇒ V max = 78732 3 π
Dấu " = " xaye ra ⇔ 3 r 2 = 162 ⇔ r = 3 6 ⇒ Độ dài cung tròn là l = 2 π r = 6 π 6
8 π chính là chu vi đường tròn đáy của cái phễu. Điều này có nghĩa là 2 πγ = 8 π ⇒ r = 4
Suy ra h = R 2 - r 2 = 5 2 - 4 2 = 3
Do đó V 1 = 1 3 . 3 π . 4 2 = 2 21 7
Đáp án B
\(3+\frac{1}{4+\frac{1}{b+\frac{1}{6}}}=\frac{421}{130}\) \(\Rightarrow\frac{1}{4+\frac{1}{b+\frac{1}{6}}}=\frac{31}{130}\Rightarrow4+\frac{1}{b+\frac{1}{6}}=\frac{130}{31}\Rightarrow\frac{1}{b+\frac{1}{6}}=\frac{6}{31}\Rightarrow b+\frac{1}{6}=\frac{31}{6}\Rightarrow b=\frac{30}{6}=5\)
Vậy b = 5
ta có \(\left|x-a\right|+\left|x-b\right|+\left|x-c\right|+\left|x-d\right|\ge\left|\left(x-a\right)+\left(x-b\right)+\left(c-x\right)+\left(d-x\right)\right|=\left|c+d-a-b\right|=c+d-a-b\)( do a<b<c<d => c-a>0 và d-b>0)
vậy Min A= c+d-a-b
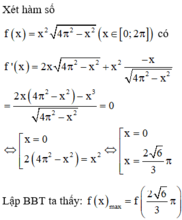
Đáp án D