Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

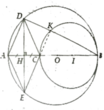
a) AB là đường kính, C thuộc đường tròn nên \(\widehat{ACB}=90^o\) hay tam giác ABC vuông tại C.
Áp dụng hệ thức lượng trong tam giác vuông, ta có
\(BC^2=MB.AB=2.6=12\Rightarrow BC=\sqrt{12}\left(cm\right)\)
b) Xét tam giác cân OAC có OE là đường cao nên đồng thời là phân giác.
Từ đó ta có \(\Delta AOE=\Delta COE\left(c-g-c\right)\Rightarrow\widehat{ECO}=\widehat{EAO}=90^o\)
Vậy EC là tiếp tuyến của (O) tại C.
c) Xét tam giác AFK, ta thấy ngay B là trực tâm nên \(AK\perp FD\). Lại có \(AD\perp FD\), vậy A, D, F thẳng hàng.
Ta thấy ngay AH là phân giác góc \(\widehat{FAK}\) mà lại là đường cao, vậy tam giác AH đồng thời là trung trực của FK.
B thuộc AH, vậy BF = BK hay tam giác FBK cân tại B.
d) Ta có tứ giác ACHK nội tiếp nên \(\widehat{HCF}=\widehat{AKF}=\widehat{AFK}\) (Tam giác AFK cân)
Ta cũng có \(\widehat{ACO}=\widehat{OAC}\)(Tam giác AOC cân)
Vậy nên \(\widehat{HCF}+\widehat{OCA}=\widehat{CHF}+\widehat{CAO}=90^o\Rightarrow\widehat{OCH}=90^o\)
Vậy thì \(\widehat{ECH}=\widehat{ECO}+\widehat{OCH}=180^o\) hay H, C, E thẳng hàng.

a: Xét (O) có
ΔACB nội tiếp
AB là đường kính
Do đó: ΔABC vuông tại C
Xét ΔCAB vuông tại C có CM là đường cao
nên \(CB^2=BM\cdot BA\)
=>\(CB=\sqrt{1\cdot6}=\sqrt{6}\left(cm\right)\)
b: ΔOAC cân tại O
mà OE là đường cao
nên OE là phân giác của \(\widehat{AOC}\)
Xét ΔOAE và ΔOCE có
OA=OC
\(\widehat{AOE}=\widehat{COE}\)
OE chung
Do đó: ΔOAE=ΔOCE
=>\(\widehat{OCE}=\widehat{OAE}=90^0\)
=>EC là tiếp tuyến của (O)

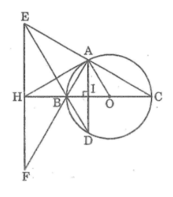
a, (O) và (I) tiếp xúc trong với nhau
b, Tứ giác ADCE là hình thoi
c, Có CK ⊥ AB, AD ⊥ DB
=> CK//AD mà CE//AD
=> B,K,D thẳng hàng
d, H K D ^ = H D K ^ ; I K B ^ = I B K ^
=> H K D ^ + I K B ^ = I B K ^ + H D K ^ = 90 0
=> I K H ^ = 90 0

a) Xét \(\Delta\) ABC có :
AB là đường kính đường tròn (O)
A,B ,C \(\varepsilon\) đường tròn (O)
=> \(\Delta\)ABC vuông tại C
Nối OC
Vì OC = OA = OA (=R)
=> OC = (AO + OB)/2
=> OC = AB/2
=> \(\Delta ABC\) vuông tại C
=> BC^2 = MB . AB
=> BC^2 = 1.6 = 6
=> BC = √6
b) Xét \(\Delta\) EAO và tam giác ECO , ta có :
OA=OC( =R)
Góc AOE = góc COE ( OE vuông góc vs AC do gt)
OE : cạnh chung
=>Tam giác EAO đồng dạng vs tam giác ECO(c.g.c)
=> góc EAO = góc ECO = 90độ (2 góc tương ứng)
=> EC vuông góc vs OC
=> EC là tiếp tuyến của đường tròn (O)


câu c yêu cầu j thế?
gọi F là giao điểm của AC và DB . Kẻ FH ⊥ AB tại H . Gọi K là giao điểm của CB và FH