Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

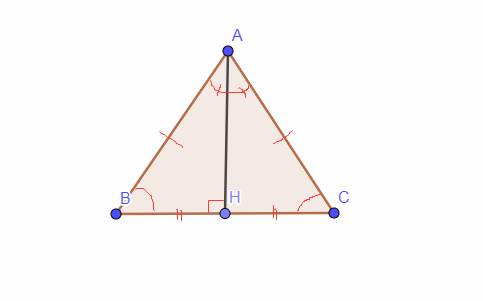
a) Xét \(\Delta ABH\) vuông tại H và \(\Delta ACH\text{vuông tại H}:\)
AB = AC \((\Delta ABC\text{cân tại A}).\)
\(\widehat{B}=\widehat{C}\) \((\Delta ABC\text{cân tại A}).\)
\(\Rightarrow\Delta ABH=\Delta ACH\) (cạnh huyền - góc nhọn).
b) Xét \(\Delta ABC\) cân tại A:
AH là đường cao \(\left(AH\perp BC\right).\)
\(\Rightarrow\) AH là phân giác \(\widehat{BAC}.\)
c) Ta có: BH = CH = \(\dfrac{1}{2}BC=\dfrac{1}{2}8=4\left(cm\right).\)
Xét \(\Delta ABH:\)
\(AB^2=AH^2+BH^2\left(Pytago\right).\\ \Rightarrow AB^2=3^2+4^2.\\ \Rightarrow AB=5\left(cm\right).\)
Mà AB = AC (\(\Delta ABC\) cân tại A).
\(\Rightarrow AC=5\left(cm\right).\)

`\color{blue}\text {#DuyNam}`
`a,` Vì Tam giác `ABC` cân `-> AB=AC,`\(\widehat{B}=\widehat{C}\)
Xét Tam giác `ABH` và Tam giác `ACH` có:
\(\widehat{B}=\widehat{C}\)
`AB = AC`
`=>` Tam giác `ABH =` Tam giác `ACH (ch-gn)`
`-> HB=HC (2` cạnh tương ứng `)`
`-> H` là trung điểm của `BC`
`b,` Vì Tam giác `ABH =` Tam giác `ACH (a)`
`->`\(\widehat{BAH}=\widehat{CAH}\) `(2` góc tương ứng `)`
`-> AH` là tia phân giác của \(\widehat{BAC}\)

Chú ý:Góc ngoài tam giác bằng tổng số đo 2 góc trog tam giác không kể với nó
Vậy góc(A1)+góc(A2)=góc(B)+góc(C) .(1)
Do Am là tia phân giác ngoài tại đỉnh A của tam giác ABC nên góc A1=góc (A2).(2)
Lại có tam giác ABC cân tại A do(AB=AC) nên góc (B)=góc(C).(3)
Từ(1);(2) và (3) =>góc(A1)+góc (A1)=góc (C)+góc(C)
Suy ra góc( A1)=góc(C) mà 2 góc này nằm ở vị ttrí so le nhau
Do đó Am//BC . (dpcm)

a: Xét ΔABH vuông tại H và ΔACH vuông tại H có
AB=AC
AH chung
Do đó: ΔABH=ΔAHC
Ta có: ΔABC cân tại A
mà AH là đường cao
nên AH là đường phân giác
b: Xét ΔADH vuông tại D và ΔAEH vuông tại E có
AH chung
\(\widehat{DAH}=\widehat{EAH}\)
Do đó: ΔADH=ΔAEH
Suy ra: HD=HE và AD=AE
d: Xét ΔABC có
AD/AB=AE/AC
nên DE//BC

a: Ta có: ΔAHB vuông tại H
=>\(AH^2+HB^2=AB^2\)
=>\(AH^2=10^2-6^2=64\)
=>\(AH=\sqrt{64}=8\left(cm\right)\)
b: Xét ΔAHB vuông tại H và ΔAHC vuông tại H có
AB=AC
AH chung
Do đó: ΔAHB=ΔAHC
=>\(\widehat{BAH}=\widehat{CAH}\)
=>AH là phân giác của góc BAC
c: Ta có: ΔAHB=ΔAHC
=>BH=CH
Xét ΔBMH vuông tại M và ΔCNH vuông tại N có
BH=CH
\(\widehat{B}=\widehat{C}\)
Do đó: ΔBMH=ΔCNH
d: Xét ΔABO vuông tại B và ΔACO vuông tại C có
AO chung
AB=AC
Do đó: ΔABO=ΔACO
=>OB=OC
=>ΔOBC cân tại O
a) Xét \(\Delta ABH\)và \(\Delta ACH\)có:
\(AB=AC\left(gt\right)\)
\(\widehat{AHB}=\widehat{AHC}\left(=90^0\right)\)
AH là cạnh chung
\(\Rightarrow\Delta ABH=\Delta ACH\left(ch.gn\right)\)
a) Vì \(\Delta ABH=\Delta ACH\left(cmt\right)\)
\(\Rightarrow\widehat{BAH}=\widehat{CAH}\)( 2 cạnh tương ứng )
=> AH là tia phân giác \(\widehat{BAC}\left(đpcm\right)\)
a:Xét tam giác ABH vuông tại H và tam giác ACH vuông tại H có
AH chung
AC =AB (giả thiết)
Suy ra tam giác ABH = tam giác ACH ( cạnh huyền cạnh góc vuông)
b:từ trên suy ra : góc CAH = góc BAH
Suy ra AH là tia phân giác của góc BAC