Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

4:
a: Xet ΔAMB và ΔAMC có
AM chung
MB=MC
AB=AC
=>ΔAMB=ΔAMC
b: Xet ΔAEM vuông tại E và ΔAFM vuông tại F có
AM chung
góc EAM=góc FAM
=>ΔAEM=ΔAFM
=>AE=AF
c: AE=AF
ME=MF
=>AM là trung trực của EF
mà K nằm trên trung trực của EF
nên A,M,K thẳng hàng

 a) Xét ∆ABD và ∆EBD có:
a) Xét ∆ABD và ∆EBD có:
AB = BE (gt)
∠ABD = ∠EBD (BD là tia phân giác của ABC)
BD là cạnh chung
⇒ ∆ABD = ∆EBD (c-g-c)
b) Do ∆ABD = ∆EBD (cmt)
⇒ AD = ED (hai cạnh tương ứng)
Lại do ∆ABD = ∆EBD (cmt)
⇒ ∠BAD = ∠BED = 90⁰ (hai góc tương ứng)
⇒ ∠DAF = ∠DEC = 90⁰
Xét hai tam giác vuông: ∆DAF và ∆DEC có:
AD = ED (cmt)
∠ADF = ∠EDC (đối đỉnh)
⇒ ∆DAF = ∆DEC (cạnh góc vuông - góc nhọn kề)
⇒ AF = EC (hai cạnh tương ứng)
c) ∆BAE có:
AB = BE (gt)
⇒ ∆BAE cân tại B
⇒ ∠BEA = ∠BAE = (180⁰ - ∠ABC) : 2 (1)
Do AF = EC (cmt)
AB = BE (gt)
⇒ AF + AB = EC + BE
⇒ BF = BC
⇒ ∆BFC cân tại B
⇒ ∠BCF = ∠BFC = (180⁰ - ∠ABC) : 2 (2)
Từ (1) và (2) suy ra:
∠BEA = ∠BCF
Mà ∠BEA và ∠BCF là hai góc đồng vị
⇒ AE // CF

a: Xét ΔABD và ΔEBD có
BA=BE
\(\widehat{ABD}=\widehat{EBD}\)
BD chung
Do đó: ΔABD=ΔEBD

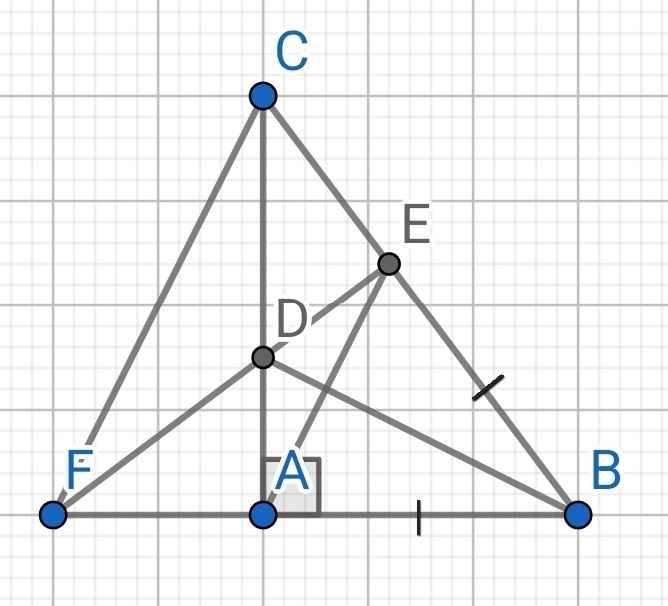
B A C D E F S
a) Tam giác ABD và EBD có:
Góc ABD = EBD (BD là phân giác)
Cạnh BA = BE (gt)
Cạnh BD chung
=> Tam giác ABD = EBD (c-g-c) (*)
b) Từ (*) => góc BED = 90 độ (= góc BAD)
=> tam giác EDC vuông tại E => cạnh huyền DC > cạnh góc vuông DE (1)
mà từ (*) => DE = AD (2)
Từ (1) và (2) => DC > AD
c) Tam giác BFC có hai đường cao CA và FE cắt nhau tại D => D là trực tâm
Đường BD đi qua trực tâm D nên là đường cao thứ ba của tam giác BFC. Đồng thời BD cũng là phân giác của góc FBC
=> tam giác FBC cân tại B => đường cao, phân giác cũng là trung tuyến. Vậy BD đi qua trung điểm S của FC.
Vậy B, D, S thẳng hàng.

e) vì AC vuông góc vs BK , KE ( kéo dài ED)vuông góc với BC mà AC và KE cắt nhau tại D => D là trực tâm của tam giác KBC => BD vuoogn góc với KC ( 1 ) .M là trung điểm của KC => BM là đường cao đồng thời là đường trung trực của tam giác KBC ( 2 ) . từ ( 1 ) và ( 2 ) => B, D , M thằng hàng

a) Xét ΔABD và ΔEBD có
BA=BE(gt)
\(\widehat{ABD}=\widehat{EBD}\)(BD là tia phân giác của \(\widehat{ABE}\))
BD chung
Do đó: ΔABD=ΔEBD(c-g-c)
b) Ta có: ΔABD=ΔEBD(cmt)
nên \(\widehat{BAD}=\widehat{BED}\)(hai góc tương ứng)
mà \(\widehat{BAD}=90^0\)(ΔABC vuông tại A)
nên \(\widehat{BED}=90^0\)

a: Xét ΔABD và ΔEBD có
BA=BE
góc ABD=góc EBD
BD chung
=>ΔBAD=ΔBED
b: ΔBAD=ΔBED
=>góc BED=góc BAD=90 độ
=>ΔBED vuông tại E
c: AD=DE
DE<DC
=>AD<DC
d: AB+EF=BE+EF
mà BE+EF>BF
nên AB+EF>BF

các bạn trả lời giúp mk vs
mai tớ giải cho