Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
2: Xét ΔEAD và ΔEBF có
góc EAD=góc EBF
góc AED=góc BEF
=>ΔEAD đồng dạng với ΔEBF
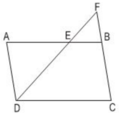
a) Áp dụng định lí: Một đường thẳng cắt hai cạnh của tam giác và song song với cạnh còn lại tạo thành một tam giác mới đồng dạng với tam giác đã cho.
ΔFCD có EB // CD (E ∈ FD, B ∈ FC)
⇒ ΔFEB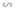 
ΔFDC (1)
ΔAED có FB // AD (F ∈ DE, B ∈ AE)
⇒ ΔFEB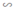 
ΔDEA (2)
Từ (1) và (2) suy ra: ΔDEA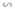 
ΔFDC (tính chất)
b) AB = 12cm, AE = 8cm
⇒ EB = AB – AE = 12 - 8 = 4cm.
Vì ABCD là hình bình hành nên AD = BC = 7cm
Do ΔFEB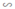 
ΔDEA
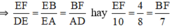
⇒ EF = 5cm, BF = 3,5cm.
a) Áp dụng định lí: Một đường thẳng cắt hai cạnh của tam giác và song song với cạnh còn lại tạo thành một tam giác mới đồng dạng với tam giác đã cho.
ΔFCD có EB // CD (E ∈ FD, B ∈ FC)
⇒ ΔFEB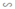 
ΔFDC (1)
ΔAED có FB // AD (F ∈ DE, B ∈ AE)
⇒ ΔFEB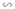 
ΔDEA (2)
Từ (1) và (2) suy ra: ΔDEA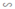 
ΔFDC (tính chất)
b) AB = 12cm, AE = 8cm
⇒ EB = AB – AE = 12 - 8 = 4cm.
Vì ABCD là hình bình hành nên AD = BC = 7cm
Do ΔFEB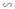 
ΔDEA
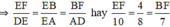
⇒ EF = 5cm, BF = 3,5cm.
a: Xét ΔFEB và ΔFDC có
góc FEB=góc FDC
góc F chung
=>ΔFEB đồng dạng với ΔFDC
Xét ΔEAD và ΔEBF có
góc EAD=góc EBF
góc AED=góc FEB
=>ΔEAD đồng dạng với ΔEBF
Xét ΔABD và ΔCDB có
góc ABD=góc CDB
góc A=góc C
=>ΔABD đồng dạng với ΔCDB
Xét ΔABC và ΔCDA có
góc ABC=góc CDA
góc BAC=góc DCA
=>ΔABC đồng dạng với ΔCDA
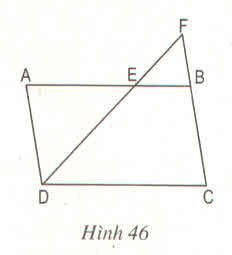
a) BE // DC => ∆BEF ∽ ∆CDF
AD // BF => ∆ADE ∽ ∆BFE.
Do đó: ∆ADE ∽ ∆CFD
b) BE = AB - AE = 12 - 8 = 4cm
∆ADE ∽ ∆BFE => =
=
=> =
=
=> BF = 3,5 cm.
EF = 5 cm.
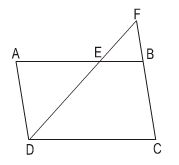
a) BE // DC => ∆BEF ∽ ∆CDF
AD // BF => ∆ADE ∽ ∆BFE.
Do đó: ∆ADE ∽ ∆CFD
b) BE = AB – AE = 12 – 8 = 4cm
∆ADE ∽ ∆BFE =>\(\frac{AE}{BE}=\frac{AD}{BF}=\frac{DE}{EF}\)
\(\Rightarrow\frac{8}{4}=\frac{7}{BF}=\frac{10}{EF}\)
\(\Rightarrow BF=3,5cm\)
\(\Rightarrow EF=5cm\)
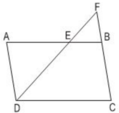
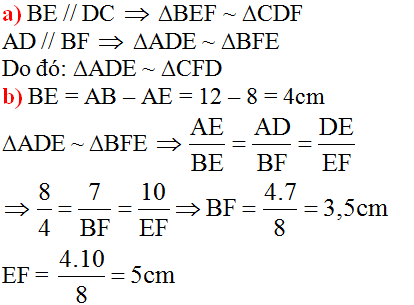
a: Xet ΔEAD và ΔEBF có
góc EAD=góc EBF
góc AED=góc BEF
=>ΔEAD đồng dạng với ΔEBF
=>AD/BF=EA/EB
=>18/BF=9/6=3/2
=>BF=12cm