Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B
Phương pháp: Xác suất : P ( A ) = n ( A ) n ( Ω )
Cách giải:
Số phần tử của không gian mẫu : n ( Ω ) = C 15 + 10 4 = C 25 4
Gọi A là biến cố : “4 học sinh được gọi đó cả nam lẫn nữ”
Khi đó :
![]()
Xác suất cần tìm:
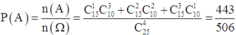

Đáp án B
Có các trường hợp sau:
+ 1 nam, 3 nữ, suy ra có C 18 1 C 17 3 cách gọi
+ 2 nam, 2 nữ, suy ra có C 18 2 C 17 2 cách gọi
+ 3 nam, 1 nữ, suy ra có C 18 3 C 17 1 cách gọi
Suy ra xác suất sẽ bằng
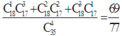

Đáp án B
Có các trường hợp sau:
+ 1 nam, 3 nữ, suy ra có C 18 1 C 17 3 cách gọi
+ 2 nam, 2 nữ, suy ra có C 18 2 C 17 2 cách gọi
+ 3 nam, 1 nữ, suy ra có C 18 3 C 17 1 cách gọi
Suy ra xác suất sẽ bằng
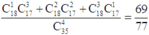

Chọn D
Gọi A là biến cố “4 học sinh được gọi có cả nam và nữ”, suy ra A ¯ là biến cố “4 học sinh được gọi toàn là nam hoặc toàn là nữ”
Số phần tử của không gian mẫu là ![]()
Ta có ![]()
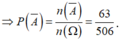
Vậy xác suất của biến cố A là
![]()

Không gian mẫu là số cách gọi ngẫu nhiên 2 nam, 2 nữ từ 46 học sinh.
Suy ra số phần tử của không gian mẫu là ![]() .
.
Gọi A là biến cố 4 học sinh (2 nam, 2 nữ) được gọi lên đều không chuẩn bị bài tập về nhà, trong đó có Bình và Mai . Ta mô tả khả năng thuận lợi cho biến cố A như sau:
● Gọi Bình và Mai lên bảng, có 1 cách.
● Tiếp theo gọi 1 bạn nam từ 6 bạn không làm bài tập về nhà còn lại và 1 bạn nữ từ 3 bạn không làm bài tập về nhà còn lại, có ![]() cách.
cách.
Suy ra số phần tử của biến cố A là 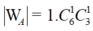 .
.
Vậy xác suất cần tính 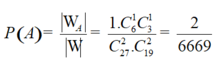 .
.
Chon C.

a) Không gian mẫu của bài toán này là tập hợp các học sinh trong tổ lớp, nó có 9 phần tử và được ký hiệu là Ω = {Hương, Hồng, Dung, Phương, Sơn, Tùng, Hoàng, Tiến, Hải}.
b) Biến cố H xảy ra khi học sinh được chọn là một bạn nữ, nó là tập hợp các học sinh nữ và được ký hiệu là
H = {Hương, Hồng, Dung, Phương}.
Biến cố K xảy ra khi học sinh được chọn có tên bắt đầu là chữ cái H, được ký hiệu là
K = {Hương, Hồng, Hoàng}.
Biến cố hợp M xảy ra khi học sinh được chọn là một bạn nữ hoặc có tên bắt đầu bằng chữ H, nó là tập hợp các học sinh trong tập H hoặc K (bao gồm cả những học sinh trùng nhau của hai tập này) và được ký hiệu là
M = H ∪ K = {Hương, Hồng, Dung, Phương, Hoàng}.
a: Ω={Hương, Hồng, Dung, Phương, Sơn, Tùng, Hoàng, Tiến, Hải}
n(Ω)=9
b: H={Hương, Hồng, Dung, Phương}
K={Hương, Hồng, Hoàng}
=>M={Hương,Hồng,Dung,Phương,Hoàng}
H là tập con của M và Ω
K là tập con của M và Ω
M là tập con của Ω

Chọn B.
Số phần tử của không gian mẫu:
![]()
Gọi A là biến cố “nhóm được chọn có cả nam và nữ, đồng thời mỗi khối có 1 học sinh nam”
⇒ số phần tử của biến cố A là: ![]()
![]() .
.

Đáp án C
Gọi ngẫu nhiên hai học sinh lên bảng trong 40 học sinh nên ta có: ![]()
Gọi biến cố A: “Trong hai bạn được gọi lên bảng, cả hai bạn đều tên là Anh”.
Trong lớp có 4 bạn tên là Anh nên ta có: ![]()
Khi đó ta có xác suất để hai bạn được gọi lên bảng đều tên là Anh là:  .
.

số cách gọi 4 hs lên bảng là: \(C^4_{25}\)Gọi A là biến cố :" bốn hs lên bảng có cả nam và nữ:
=> ta phải tính n(A)=?
phương án 1; 3 nam và 1 nữ: \(C^3_{15}.C^1_{10}=4550\)
phương án 2: 2 nam và 2 nữ : \(C^1_{15}.C^2_{10}=4725\)
phương án 3: 1 nam vfa 3 nữ: \(C^1_{15}.C^3_{10}=1800\)
=> n(A)=4550+4725+1800=11075 cách
=> p(A)=\(\frac{11075}{C^4_{25}}=\frac{443}{506}\)
chue yếu bạn áp dụng các quy tắc cộng và nhân là xong