Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Ta có: ΔABC cân tại A
mà AH là đường cao
nên H là trung điểm của BC
b: BH=CH=BC/2=6cm
=>AH=8cm
c: Xét ΔAEH có
AK là đường cao
AK là đường trung tuyến
Do đó: ΔAEH cân tại A
hay AH=AE(1)
Xét ΔADH có
AI là đường cao
AI là đường trung tuyến
Do đó; ΔADH cân tại A
hay AD=AH(2)
Từ (1) và (2) suy ra AD=AE
hay ΔADE cân tại A
d: Xét ΔAHI vuông tại I và ΔAHK vuông tại K có
AH chung
\(\widehat{IAH}=\widehat{KAH}\)
Do đó: ΔAHI=ΔAHK
Suy ra: HI=HK
=>HD=HE
hay H nằm trên đường trung trực của DE(3)
Ta có: AD=AE
nên A nằm trên đường trung trực của DE(4)
Từ (3) và (4) suy ra AH là đường trung trực của DE

a) Xét tam giác ABH và tam giác ACH có
AB=AC (tam giác ABC cân tại A)
\(\widehat{ABH}=\widehat{ACH}\)(tam giác ABC cân tại A)
BH=HC(H là trung điểm BC)
=> Tam giác ABH = Tam giác ACH (cgc)
b) Vì tam giác ABC cân tại A (gt) và H là trung điểm BC(gt)
=> AH là đường trung tuyến đồng thời là đường cao của tam giác ABC
=> AH vuông góc với BC(đpcm)
a) Xét t/giác ABH và t/giác ACH
c: AB = AC (gt)
BH = CH (gt)
AH: chung
=> t/giác ABH = t/giác ACH (c.c.c)
b) Ta có: t/giác ABH = t/giác ACH (cmt)
=> \(\widehat{AHB}=\widehat{AHC}\)(2 góc t/ứng)
mà \(\widehat{AHB}+\widehat{AHC}=180^0\)(kề bù)
=> \(\widehat{AHB}=\widehat{AHC}=90^0\)
=> AH \(\perp\)BC
c) Ta có: BH = CH = 1/BC = 1/2.6 = 3 (cm)
Áp dụng định lí Pi - ta - go vào t/giác ABH vuông tại H, ta có:
AB2 = AH2 + BH2 => AH2 = 52 - 32 = 16
=> AH = 4 (cm)
d) Ta có: t/giác AHB = t/giác AHC (cmt)
=> \(\widehat{A_1}=\widehat{A_2}\) (2 góc t/ứng)
Xét t/giác AHE và t/giác AHK
có: \(\widehat{A_1}=\widehat{A_2}\)(cmt)
AH : chung
\(\widehat{AEH}=\widehat{AKH}=90^0\)(gt)
=> t/giác AHE = t/giác AHK (ch - gn)
=> HE = HK (2 cạnh t/ứng)
e) Ta có: t/giác AHE = t/giác AHK (cmt)
=> AE = AK (2 cạnh t/ứng)
=> t/giác AEK cân tại A
=> \(\widehat{AEK}=\widehat{AKE}=\frac{180^0-\widehat{A}}{2}\)(1)
T/giác ABC cân tại A
=> \(\widehat{B}=\widehat{C}=\frac{180^0-\widehat{A}}{2}\)(2)
Từ (1) và (2) => \(\widehat{AEK}=\widehat{B}\)
Mà 2 góc này ở vị trí đồng vị
=> EK // BC

a, Xét tam giác ABC cân tại A có
AH là đường cao đồng thời là đường trung tuyến, là đường phân giác
=> HB = HC
b, Xét tam giác HIA và tam giác HKA có
AH _ chung ; ^HAI = ^HAK ( do AH là phân giác cma )
Vậy tam giác HIA = tam giác HKA (ch-gn)
=> HI = HK (2 cạnh tương ứng)
Xét tam giác IHK có HI = HK
Vậy tam giác IHK cân tại H

Xét \(\Delta ABH\)và \(\Delta ACH\)có:
\(AB=AC\)( \(\Delta ABC\)cân tại A )
AH là cạnh chung
\(\widehat{AHB}=\widehat{AHC}\left(=90^0\right)\)
\(\Rightarrow\Delta ABH=\Delta ACH\left(ch.gn\right)\)
\(\Rightarrow HB=HC\)( 2 cạnh tương ứng )
b) Vì \(HB=HC\left(cmt\right)\)
\(\Rightarrow HB=HC=\frac{12}{2}=6cm\)
Xét \(\Delta ACH\left(\widehat{H}=90^0\right)\) có:
\(AC^2=AH^2+CH^2\)( định lý py-ta-go )
\(\Rightarrow10^2=AH^2+6^2\)
\(\Rightarrow AH^2=10^2-6^2\)
\(\Rightarrow AH^2=64\)
\(\Rightarrow AH=\sqrt{64}\)
\(\Rightarrow AH=8cm\)
Vậy \(AH=8cm\)
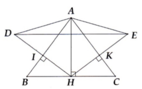



a: Xét ΔBHA vuông tại H có
\(BA^2=BH^2+HA^2\)
hay AH=3(cm)
b: Xét ΔABH vuông tại H và ΔCBH vuông tại H có
BA=BC
BH chung
Do đó: ΔABH=ΔCBH
c: Xét ΔBIH vuông tại I và ΔBKH vuông tại K có
BH chung
\(\widehat{IBH}=\widehat{KBH}\)
Do đó: ΔBIH=ΔBKH
Suy ra: HI=HK
d: Xét ΔBAC có BI/BA=BK/BC
Do đó: IK//AC