Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Xét tam giác ABC, có:
* D, E lần lượt là trung điểm của AB, AC (gt)
=> DE là đường trung bình của tam giác ABC
=> DE // BC
=> DE = 1/2 BC = 1/2 . 8 = 4 (cm)
Ta có: DE // BC (cmt)
=> DECB là hình thang
Xét hình thang DECB (DE // BC), có:
* M, N lần lượt là trung điểm của DB, EC (gt)
=> MN là đường trung bình của hình thang DECB
=> MN = (DE + BC) : 2 = (4+8) : 2 = 6 (cm)
Cho tam giác ABC có BC = 8cm. Gọi D và E lần lượt là trung điểm các cạnh AB, AC. M và N lần lượt là trung điểm của BD và CE. Khi đó MN =.........cm
Xét tam giác ABC, có:
* D, E lần lượt là trung điểm của AB, AC (gt)
=> DE là đường trung bình của tam giác ABC
=> DE // BC
=> DE = 1/2 BC = 1/2 . 8 = 4 (cm)
Ta có: DE // BC (cmt)
=> DECB là hình thang
Xét hình thang DECB (DE // BC), có:
* M, N lần lượt là trung điểm của DB, EC (gt)
=> MN là đường trung bình của hình thang DECB
=> MN = (DE + BC) : 2 = (4+8) : 2 = 6 (cm)
nhé !

a: Xét ΔABC có
\(\dfrac{AD}{AB}=\dfrac{AE}{AC}\)
Do đó: DE//BC
Xét tứ giác BDEC có DE//BC
nên BDEC là hình thang
mà \(\widehat{B}=\widehat{C}\)
nên BDEC là hình thang cân

A B C D E M N 18 cm
D và E là trung điểm của AB và AC => DE là đường trung bình của tam giác ABC
=> DE//BC và DE=1/2 BC = 9cm
Tứ giác DECB có DE // BC => Hình thang DECB đáy DE, CB
Lại có M, N là trung điểm BD và CE=> MN là đường trung bình của hình thang DECB
=> MN = 1/2 ( DE + BC) = 1/2 (9+18) = 13,5 (cm)
Vậy....................................
________________________JK~ Liên Quân Group ________________________

* Xét tam giác ABC có D và E lần lượt là trung điểm của AB và AC nên DE là đường trung bình của tam giác.
Suy ra: DE// BC và
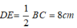
* Xét tứ giác DECB có DE // BC nên DECB là hình thang.
Lại có: M và N lần lượt là trung điểm của BD và EC nên MN là đường trung bình của hình thang .

Chọn đáp án D

a: Xét ΔABC có
D là trung điểm của AB
E là trung điểm của AC
Do đó: DE là đường trung bình của ΔBAC
Suy ra: \(DE=\dfrac{BC}{2}=4\left(cm\right)\)
a: Xét hình thang BDEC có
M là trung điểm của BD
N là trung điểm của EC
Do đó: MN là đường trung bình của hình thang BDEC
Suy ra: \(MN=\dfrac{DE+BC}{2}=\dfrac{8+4}{2}=6\left(cm\right)\)