Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a, Xét tam giác AHB và tam giác AKC có
^A_chung
AB = AC
Vậy tam giác AHB ~ tam giác AKC ( ch-gn )
=> AH = AK ( 2 cạnh tương ứng )
b, Xét tam giác ABC cân tại A
có BH ; CK lần lượt là đường cao
mà BK giao CK = D vậy D là trực tâm
hay AD là đường cao thứ 3 trong tam giác
=> AD đồng thời là đường phân giác
c, Ta có AH = AK ; AB = AC
=> HK // BC ( Ta lét đảo _)

a: Xét ΔABH vuông tại H và ΔACK vuông tại K có
AB=AC
\(\widehat{BAH}\) chung
Do đó: ΔABH=ΔACK
Suy ra: AH=AK
b: Xét ΔAKI vuông tại K và ΔAHI vuông tại H có
AI chung
AK=AH
Do đó: ΔAKI=ΔAHI
Suy ra: \(\widehat{KAI}=\widehat{HAI}\)
hay AI là tia phân giác của góc BAC
c: Xét ΔKBC vuông tại K và ΔHCB vuông tại H có
BC chung
KC=HB
Do đó: ΔKBC=ΔHCB
Suy ra: \(\widehat{IBC}=\widehat{ICB}\)
hay ΔIBC cân tại I
d: Xét ΔABC có AK/AB=AH/AC
nên KH//BC
e: Ta có: ΔABC cân tại A
mà AI là đường phân giác
nên AI là đường cao

Hình tự vẽ nha bạn
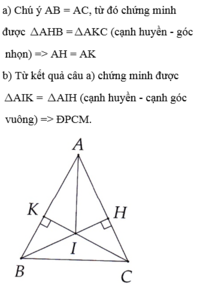
a) Xét \(\Delta AHB\)và \(\Delta AKC\)có:
\(\hept{\begin{cases}\widehat{A}:chung\\AB=AC\left(gt\right)\\\widehat{AHB}=\widehat{AKC}\left(gt\right)\end{cases}}\)
\(\Rightarrow\Delta AHB=\Delta AKC\left(ch-gn\right)\)
=>AH=AK ( 2 cạnh tương ứng) -đpcm
b) Xét \(\Delta AKI\)và \(\Delta AHI\)có:
\(\hept{\begin{cases}AK=AH\\\widehat{AKI}=\widehat{AHI}\\AI:chung\end{cases}}\)
\(\Rightarrow\Delta AKI=\Delta AHI\left(ch-cgv\right)\)
\(\Rightarrow\widehat{IAK}=\widehat{IAH}\)( 2 góc tương ứng)
=> AI là ti phân giác góc KAH
Xét \(\Delta KAH\)cân tại A ( do AH=AK ) có AI là tia phân giác ứng cạnh KH
=> AI đồng thời là đường trung trực của cạnh KH (t/c) -đpcm
c) Kẻ CM \(\perp\)BE
Xét tứ giác BKCM có:
\(\hept{\begin{cases}\widehat{CKB}=90^0\\\widehat{KBM}=90^0\\\widehat{BMC}=90^0\end{cases}}\)
=> tứ giác BKCM là hình chữ nhật (dấu hiệu nhận biết)
=> BK=CM (t/c) (1)
Dễ dàng chứng minh đc: BK=CH (2)
Từ (1) và (2) có : CM=CH
Xét \(\Delta BHC\)và \(\Delta BMC\)có:
\(\hept{\begin{cases}CH=CM\\\widehat{BHC}=\widehat{BMC}\\CB:chung\end{cases}}\)
=> \(\Delta BHC=BMC\left(ch-cgv\right)\)
=> \(\widehat{CBH}=\widehat{CBM}\)(2 góc tương ứng)
=> BC là tia phân giác góc HBM
hay BC là tia phân giác HBE -đpcm
Chúc bạn học tốt!
d) Xét tam giác CME vuông tại M có CE là cạnh huyền
=>CE>CM (trong tam giác vuông cạnh huyền là cạnh lớn nhất)
mà CH=CM do \(\Delta CBH=\Delta CBM\)
=>CE>CH

Lời giải:
a. Xét tam giác $ABH$ và $ACK$ có:
$AB=AC$
$\widehat{A}$ chung
$\widehat{AHB}=\widehat{AKC}=90^0$
$\Rightarrow \triangle ABH=\triangle ACK$ (ch-gn)
$\Rightarrow AH=AK$
b.
Từ tam giác bằng nhau phần a suy ra $\widehat{B_1}=\widehat{C_1}$
Vì $AB=AC; AK=AH\Rightarrow AB-AK=AC-AH$
$\Rightarrow BK=CH$
Xét tam giác $KBI$ và $HCI$ có:
$\widehat{B_1}=\widehat{C_1}$
$\widehat{BKI}=\widehat{CHI}=90^0$
$BK=CH$
$\Rightarrow \triangle KBI=\triangle HCI$ (c.g.c)
$\Rightarrow BI=CI$
Xét tam giác $ABI$ và $ACI$ có:
$AB=AC$
$AI$ chung
$BI=CI$
$\Rightarrow \triangle ABI=\triangle ACI$ (c.c.c)
$\Rightarrow \widehat{BAI}=\widehat{CAI}$
$\Rightarrow AI$ là phân giác $\widehat{A}$
$



 hãy cho mk 1 L-I-K-E
hãy cho mk 1 L-I-K-E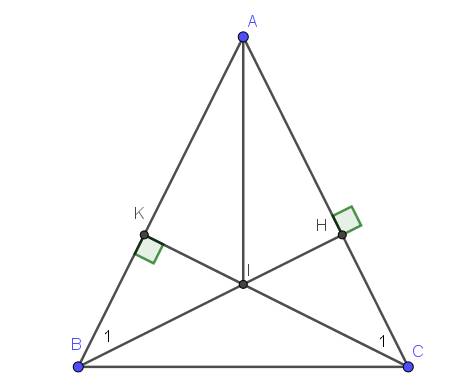
a: Xét ΔABH vuông tại H và ΔACK vuông tại K có
AB=AC
\(\widehat{BAH}\) chung
Do đó:ΔABH=ΔACK
Suy ra: AH=AK
b: Xét ΔKBC vuông tại K và ΔHCB vuông tại H có
BC chung
KC=HB
Do đó:ΔKBC=ΔHCB
Suy ra: \(\widehat{MBC}=\widehat{MCB}\)
hayΔMBC cân tại M
Xét ΔABM và ΔACM có
AB=AC
AM chung
BM=CM
Do đó:ΔABM=ΔACM
Suy ra: \(\widehat{BAM}=\widehat{CAM}\)
hay AM là tia phân giác của góc A
c: Xét ΔABC có AK/AB=AH/AC
nên KH//BC