Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a:Xét ΔMQN vuông tại Q và ΔMQE vuông tại Q có
QN=QE
MQ chung
Do đó: ΔMQN=ΔMQE
b: ta có: ΔMQN=ΔMQE
nên MN=ME
=>ΔMNE cân tại M
mà \(\widehat{N}=60^0\)
nên ΔMNE đều
a, Xét Δ MQN và Δ MQE, có :
\(\widehat{MQN}=\widehat{MQE}=90^o\)
QN = QE (gt)
MQ là cạnh chung
=> Δ MQN = Δ MQE (c.g.c)
b, Ta có : Δ MQN = Δ MQE (cmt)
=> MN = ME
=> Δ MNE cân tại M
Xét Δ MNP vuông tại N, có :
\(\widehat{NMP}+\widehat{MPN}+\widehat{PNM}=180^o\)
=> \(\widehat{PNM}=90^o-30^o\)
=> \(\widehat{PNM}=60^o\)
Mà Δ MNE cân tại M
=> ΔMNE đều

a: Xét ΔCDH vuông tại H và ΔCAH vuông tại H có
CH chung
HD=HA
Do đó: ΔCDH=ΔCAH
b: Xét ΔCDA có CD=CA
nên ΔCDA cân tại C
mà \(\widehat{D}=60^0\)
nên ΔCDA đều

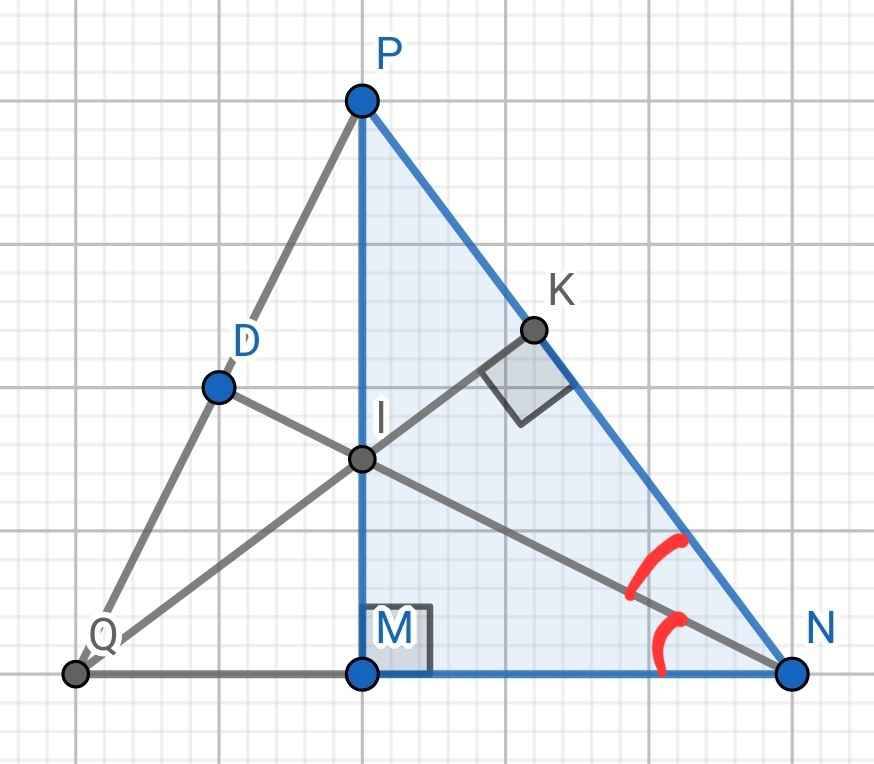
a) Xét hai tam giác vuông: ∆IMN và ∆IKN có:
IN chung
MNI = KNI (do NI là phân giác của ∠MNP)
⇒ ∆IMN = ∆IKN (cạnh huyền - góc nhọn)
b) ∆IKP vuông tại K
IP là cạnh huyền nên IP lớn nhất
IK < IP (1)
Do ∆IMN = ∆IKN (cmt)
⇒ MI = IK (2)
Từ (1) và (2)⇒ MI < IP
c) Xét hai tam giác vuông: ∆IKP và ∆IMQ có:
IM = IK (cmt)
∠PIK = ∠MIQ (đối đỉnh)
∆IKP = ∆IMQ (cạnh góc vuông - góc nhọn kề)
⇒ KP = MQ (hai cạnh tương ứng) (3)
Do ∆IMN = ∆IKN (cmt)
⇒ MN = KN (hai cạnh tương ứng) (4)
Từ (3) và (4) ⇒ KN + KP = MN + MQ
NP = NQ
⇒ ∆NPQ cân tại N
Lại có NI là phân giác của ∠MNP
⇒ NI là phân giác của ∠QNP
⇒ NI cũng là đường cao của ∆NPQ (tính chất tam giác cân)
⇒ ND ⊥ QP

a, xét tma giác MNE và tam giác MPE có :
MN = MP và góc MNE = góc MPE do tam giác MNP cân tại M (Gt)
NE = EP do E là trđ của NP (gt)
=> tam giác MNE = tam giác MPE (c-g-c)
=> góc MEN = góc MEP (đn)
mà góc MEN + góc MEP = 180 (kb)
=> góc MEN = 90
=> MN _|_ NP và có M là trđ của PN (Gt)
=> ME là trung trực của NP (đn)
b, xét tam giác MKE và tam giác MHE có : ME chung
góc NME = góc PME do tam giác MNE = tam giác MPE (Câu a)
góc MKE = góc MHE = 90
=> tam giác MKE = tam giác MHE (ch-cgv)
=> MK = MH (đn)
=> tam giác MHK cân tại M (đn)
=> góc MKH = (180 - góc NMP) : 2 (tc)
tam giác MNP cân tại M (Gt) => góc MNP = (180 - góc NMP) : 2 (tc)
=> góc MKH = góc MNP mà 2 góc này đồng vị
=> KH // NP (đl)
a Xet ΔMQN vuông tại Q và ΔMQE vuông tại Q có
MQ chung
QN=QE
=>ΔMQN=ΔMQE
b: Xet ΔMEN có
MN=ME
góc N=60 độ
=>ΔMEN đều