Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

x ∈ BC(15;35;42) và 250 < x < 850
Ta có BCNN(15;35;42) = 210
x ∈ {0;210;420;630;840;1050;...}
Vì và 250 < x < 850 nên x ∈ {420;630;840}

theo bào cho ta có : \(x\in BC\left(15;35;42\right)=\left\{210;420;630;840;.....\right\}\)
mà \(250< x< 850\Rightarrow x\in\left\{420;630;840\right\}\)
theo bài ta có:
x chia hết cho 15
x chia hết cho 35 ==> x thuộc BC(15,35,42)
x chia hết cho 42
15=3X5
35=5X7
42=2X3X7
BCNN(15,35,42)=2X3X5X7=210
BC(15,35,42)=[0,210,420,630,840,.....]
mà 250<x<850 nên x=420,630,840.
NẾU BẠN THẤY ĐÚNG THÌ K CHO MÌNH NHÉ!

a, a = BCNN(15;115) = 345
b, a – 1 ∈ BC(35;52) và 999 < a – 1 < 1999
Ta có BCNN(35;52) = 35.52 = 1820
Suy ra a – 1 ∈ {0;1820;3640;...}
Vì 999 < a – 1 < 1999 nên a – 1 = 1820
a = 1821

mmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmm

a: \(35=5\cdot7;105=3\cdot5\cdot7\)
=>\(ƯCLN\left(35;105\right)=35\)
\(35⋮x;105⋮x\)
=>\(x\inƯC\left(35;105\right)\)
mà x lớn nhất
nên x=ƯLCN(35;105)
=>x=35
b:
\(72=2^3\cdot3^2;54=3^3\cdot2\)
=>\(ƯCLN\left(72;54\right)=3^2\cdot2=18\)
\(72⋮x;54⋮x\)
=>\(x\inƯC\left(72;54\right)\)
=>\(x\inƯ\left(18\right)\)
=>\(x\in\left\{1;-1;2;-2;3;-3;6;-6;9;-9;18;-18\right\}\)
mà 10<x<20
nên x=18
c:
\(21=3\cdot7;35=5\cdot7;50=5^2\cdot2\)
=>\(BCNN\left(21;35;50\right)=5^2\cdot2\cdot3\cdot7=1050\)
\(x⋮21;x⋮35;x⋮50\)
=>\(x\in BC\left(21;35;50\right)\)
=>\(x\in B\left(1050\right)\)
mà x nhỏ nhất
nên x=1050
d:
\(39=3\cdot13;65=5\cdot13;26=2\cdot13\)
=>\(BCNN\left(39;65;26\right)=2\cdot3\cdot5\cdot13=390\)
\(x⋮39;x⋮65;x⋮26\)
=>\(x\in BC\left(39;65;26\right)\)
=>\(x\in B\left(390\right)\)
=>\(x\in\left\{390;780;1170;...\right\}\)
mà 100<=x<=999
nên \(x\in\left\{390;780\right\}\)


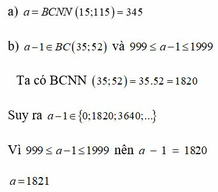
a) \(x⋮15;x⋮35;x⋮42\&250< x< 850\) (sửa dấu chia thành chia hết)
\(BCNN\left(15;35;42\right)=210\)
\(\Rightarrow x\in BC\left(15;35;42\right)=\left\{0;210;420;630;840;...\right\}\)
mà \(250< x< 850\)
\(\Rightarrow x\in\left\{420;630;840\right\}\)
b) x nhỏ nhất khác 0 thỏa mãn \(x⋮15;x⋮115\)
\(BCNN\left(15;115\right)=345\)
Vậy \(x\in\left\{345\right\}\) thỏa mãn đề bài
Bài c bạn xem lại đề