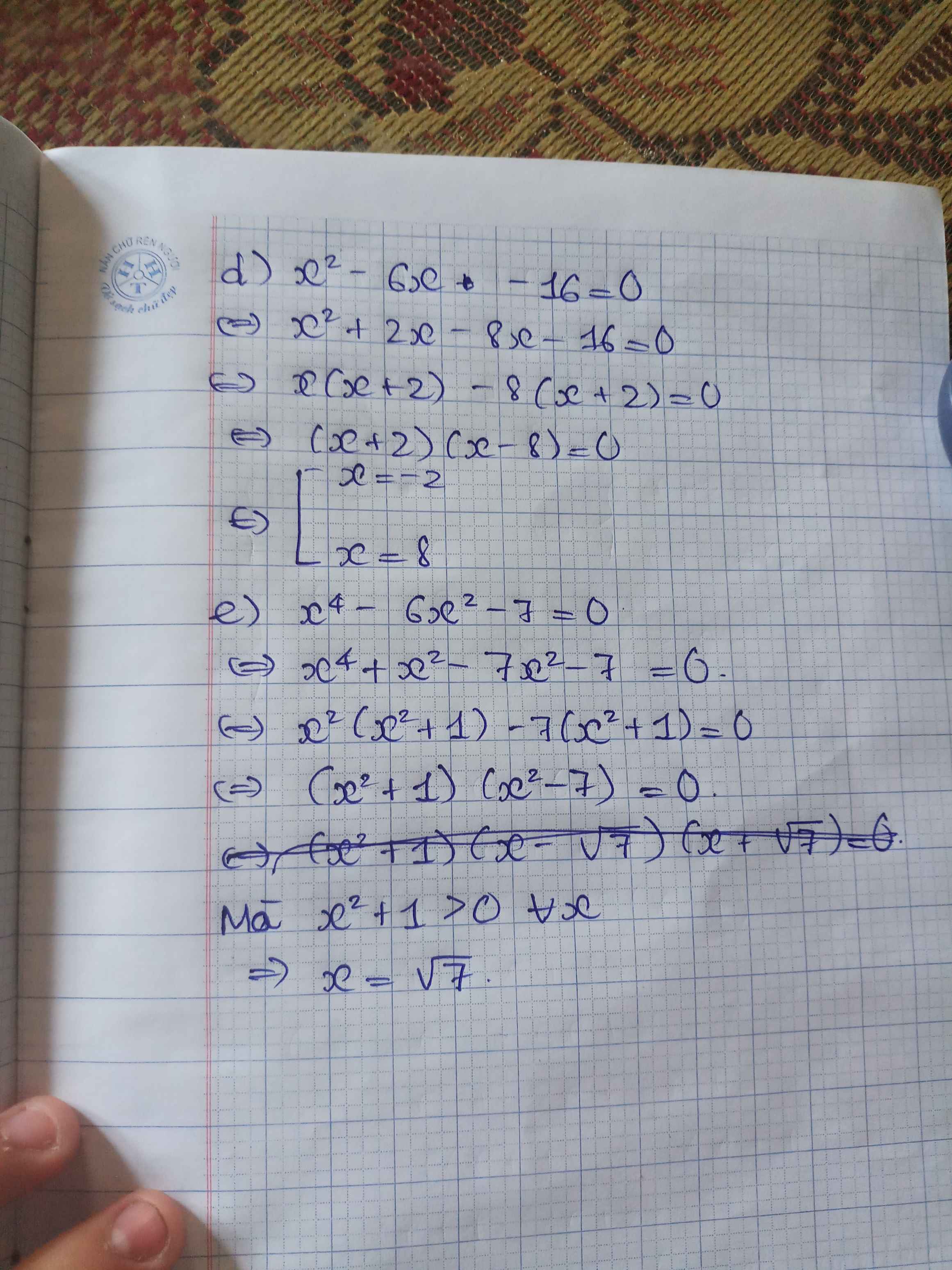Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) \(x^3-x^2+3x-3>0\)
\(\Leftrightarrow x^2\left(x-1\right)+3\left(x-1\right)>0\)
\(\Leftrightarrow\left(x^2+3\right)\left(x-1\right)>0\)
Mà: \(x^2+3>0\forall x\)
\(\Leftrightarrow x-1>0\)
\(\Leftrightarrow x>1\)
b) \(x^3+x^2+9x+9< 0\)
\(\Leftrightarrow x^2\left(x+1\right)+9\left(x+1\right)< 0\)
\(\Leftrightarrow\left(x^2+9\right)\left(x+1\right)< 0\)
Mà: \(x^2+9>0\forall x\)
\(\Leftrightarrow x+1< 0\)
\(\Leftrightarrow x< -1\)
d) \(4x^3-14x^2+6x-21< 0\)
\(\Leftrightarrow2x^2\left(2x-7\right)+3\left(2x-7\right)< 0\)
\(\Leftrightarrow\left(2x^2+3\right)\left(2x-7\right)< 0\)
Mà: \(2x^2+3>0\forall x\)
\(\Leftrightarrow2x-7< 0\)
\(\Leftrightarrow2x< 7\)
\(\Leftrightarrow x< \dfrac{7}{2}\)
d) \(x^2\left(2x^2+3\right)+2x^2>-3\)
\(\Leftrightarrow2x^4+3x^2+2x^2+3>0\)
\(\Leftrightarrow2x^4+5x^2+3>0\)
\(\Leftrightarrow\left(x^2+1\right)\left(2x^2+3\right)>0\)
Mà:
\(x^2+1>0\forall x\)
\(2x^2+3>0\forall x\)
\(\Rightarrow x\in R\)
a: =>x^2(x-1)+3(x-1)>0
=>(x-1)(x^2+3)>0
=>x-1>0
=>x>1
b: =>x^2(x+1)+9(x+1)<0
=>(x+1)(x^2+9)<0
=>x+1<0
=>x<-1
c: 4x^3-14x^2+6x-21<0
=>2x^2(2x-7)+3(2x-7)<0
=>2x-7<0
=>x<7/2
d: =>x^2(2x^2+3)+2x^2+3>0
=>(2x^2+3)(x^2+1)>0(luôn đúng)

a: ta có: \(x^2+3x-\left(2x+6\right)=0\)
\(\Leftrightarrow\left(x+3\right)\left(x-2\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-3\\x=2\end{matrix}\right.\)
b: Ta có: \(5x+20-x^2-4x=0\)
\(\Leftrightarrow\left(x+4\right)\left(5-x\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-4\\x=5\end{matrix}\right.\)

a) Ta có: \(x^3+x^2+x+1=0\)
\(\Leftrightarrow x^2\left(x+1\right)+\left(x+1\right)=0\)
\(\Leftrightarrow\left(x+1\right)\left(x^2+1\right)=0\)
mà \(x^2+1>0\forall x\)
nên x+1=0
hay x=-1
Vậy: S={-1}
b) Ta có: \(x^3-6x^2+11x-6=0\)
\(\Leftrightarrow x^3-x^2-5x^2+5x+6x-6=0\)
\(\Leftrightarrow x^2\left(x-1\right)-5x\left(x-1\right)+6\left(x-1\right)=0\)
\(\Leftrightarrow\left(x-1\right)\left(x^2-5x+6\right)=0\)
\(\Leftrightarrow\left(x-1\right)\left(x-2\right)\left(x-3\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x-1=0\\x-2=0\\x-3=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=1\\x=2\\x=3\end{matrix}\right.\)
Vậy: S={1;2;3}
c) Ta có: \(x^3-x^2-21x+45=0\)
\(\Leftrightarrow x^3-3x^2+2x^2-6x-15x+45=0\)
\(\Leftrightarrow x^2\left(x-3\right)+2x\left(x-3\right)-15\left(x-3\right)=0\)
\(\Leftrightarrow\left(x-3\right)\left(x^2+2x-15\right)=0\)
\(\Leftrightarrow\left(x-3\right)\left(x^2+5x-3x-15\right)=0\)
\(\Leftrightarrow\left(x-3\right)^2\cdot\left(x+5\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x-3=0\\x+5=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=3\\x=-5\end{matrix}\right.\)
Vậy: S={3;-5}
d) Ta có: \(x^4+2x^3-4x^2-5x-6=0\)
\(\Leftrightarrow x^4-2x^3+4x^3-8x^2+4x^2-8x+3x-6=0\)
\(\Leftrightarrow x^3\left(x-2\right)+4x^2\cdot\left(x-2\right)+4x\left(x-2\right)+3\left(x-2\right)=0\)
\(\Leftrightarrow\left(x-2\right)\left(x^3+4x^2+4x+3\right)=0\)
\(\Leftrightarrow\left(x-2\right)\left(x^3+3x^2+x^2+4x+3\right)=0\)
\(\Leftrightarrow\left(x-2\right)\left[x^2\left(x+3\right)+\left(x+1\right)\left(x+3\right)\right]=0\)
\(\Leftrightarrow\left(x-2\right)\left(x+3\right)\left(x^2+x+1\right)=0\)
mà \(x^2+x+1>0\forall x\)
nên (x-2)(x+3)=0
\(\Leftrightarrow\left[{}\begin{matrix}x-2=0\\x+3=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=2\\x=-3\end{matrix}\right.\)
Vậy: S={2;-3}

\(a)x^2-9x+20=0 \\<=>(x-4)(x-5)=0 \\<=>x=4\ hoặc\ x=5 \\b)x^2-3x-18=0 \\<=>(x+3)(x-6)=0 \\<=>x=-3\ hoặc\ x=6 \\c)2x^2-9x+9=0 \\<=>(x-3)(2x-3)=0 \\<=>x=3\ hoặc\ x=\dfrac{3}{2}\)
d: \(\Leftrightarrow3x^2-6x-2x+4=0\)
=>(x-2)(3x-2)=0
=>x=2 hoặc x=2/3
e: \(\Leftrightarrow3x\left(x^2-2x-3\right)=0\)
=>x(x-3)(x+1)=0
hay \(x\in\left\{0;3;-1\right\}\)
f: \(\Leftrightarrow x^2-5x-2+x=0\)
\(\Leftrightarrow x^2-4x-2=0\)
\(\Leftrightarrow\left(x-2\right)^2=6\)
hay \(x\in\left\{\sqrt{6}+2;-\sqrt{6}+2\right\}\)

6: \(-x^2y\left(xy^2-\dfrac{1}{2}xy+\dfrac{3}{4}x^2y^2\right)\)
\(=-x^3y^3+\dfrac{1}{2}x^3y^2-\dfrac{3}{4}x^4y^3\)
7: \(\dfrac{2}{3}x^2y\cdot\left(3xy-x^2+y\right)\)
\(=2x^3y^2-\dfrac{2}{3}x^4y+\dfrac{2}{3}x^2y^2\)
8: \(-\dfrac{1}{2}xy\left(4x^3-5xy+2x\right)\)
\(=-2x^4y+\dfrac{5}{2}x^2y^2-x^2y\)
9: \(2x^2\left(x^2+3x+\dfrac{1}{2}\right)=2x^4+6x^3+x^2\)
10: \(-\dfrac{3}{2}x^4y^2\left(6x^4-\dfrac{10}{9}x^2y^3-y^5\right)\)
\(=-9x^8y^2+\dfrac{5}{3}x^6y^5+\dfrac{3}{2}x^4y^7\)
11: \(\dfrac{2}{3}x^3\left(x+x^2-\dfrac{3}{4}x^5\right)=\dfrac{2}{3}x^3+\dfrac{2}{3}x^5-\dfrac{1}{2}x^8\)
12: \(2xy^2\left(xy+3x^2y-\dfrac{2}{3}xy^3\right)=2x^2y^3+6x^3y^3-\dfrac{4}{3}x^2y^5\)
13: \(3x\left(2x^3-\dfrac{1}{3}x^2-4x\right)=6x^4-x^3-12x^2\)

a, \(x^4-x^2-2=0\Leftrightarrow x^4-2x^2+x^2-2=0\)
\(\Leftrightarrow x^2\left(x^2-2\right)+\left(x^2-2\right)=0\Leftrightarrow\left(x^2+1>0\right)\left(x^2-2\right)=0\Leftrightarrow x=\pm\sqrt{2}\)
b, \(\Leftrightarrow x^2\left(x^2+2x+1\right)=0\Leftrightarrow x^2\left(x+1\right)^2=0\Leftrightarrow x=0;x=-1\)
c, \(\Leftrightarrow\left(x-1\right)\left(x^2+x+1>0\right)=0\Leftrightarrow x=1\)
d, \(\Leftrightarrow6x^2-3x-4x+2=0\Leftrightarrow\left(3x-2\right)\left(2x-1\right)=0\Leftrightarrow x=\dfrac{2}{3};x=\dfrac{1}{2}\)
a)
/ \(x^4+x^2-2=0\)
\(\Leftrightarrow\left(x^2\right)^2-x^2+2x^2-2=0\\ \Leftrightarrow x^2\left(x^2-1\right)+2\left(x^2-1\right)=0\\ \Leftrightarrow\left(x^2+2\right)\left(x^2-1\right)=0\\ \Leftrightarrow\left(x^2+2\right)\left(x-1\right)\left(x+1\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x^2+2=0\\x+1=0\\x-1-0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=1\\x=-1\end{matrix}\right.\)

a: =>2x^2+9x-6x-27=0
=>x(2x+9)-3(2x+9)=0
=>(2x+9)(x-3)=0
=>x=3 hoặc x=-9/2
b: =>-10x^2+6x-5x+3=0
=>-2x(5x-3)-(5x-3)=0
=>(5x-3)(-2x-1)=0
=>x=-1/2 hoặc x=5/3
c: =>-x^3+2x^2-x^2+4=0
=>-x^2(x-2)-(x-2)(x+2)=0
=>(x-2)(-x^2-x-2)=0
=>x-2=0
=>x=2
d: =>(x^3+8)-4x(x+2)=0
=>(x+2)(x^2-2x+4)-4x(x+2)=0
=>(x+2)(x^2-6x+4)=0
=>x=-2 hoặc \(x=3\pm\sqrt{5}\)