Question

[Nguyễn Quốc Huy]

Bài 1:*Tìm số tự nhiên n biết :

a)4n+3 chia hết cho 2n+1

b)n+3 chia hết cho n-1

Answer 1

[Hằng Phạm]

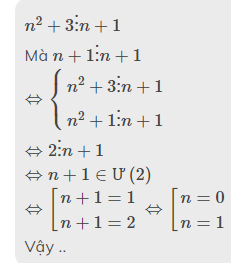
\(\frac{4n+3}{2n+1}=\frac{4n+4-1}{2n+1}=\frac{2\left(2n+1\right)-1}{2n+1}\Rightarrow\inƯ\left(1\right)\)

\(\frac{n+3}{n-1}=\frac{n-1+4}{n-1}\Rightarrow\inƯ\left(4\right)\)
Rồi bạn tự làm ra nhé

Answer 2

[Trần Hùng Minh]

a) Ta có :

4n + 3 chia hết cho 2n + 1

=> 4n + 2 + 1 chia hết cho 2n + 1 (1)

Mà 4n + 2 chia hết cho 2n + 1 (2)

Từ (1) và (2) suy ra :

1 chia hết cho 2n + 1

=> 2n + 1 \(\in\) Ư(1) = {1}

=> 2n + 1 = 1

=> 2n = 0

=> n = 0.

Vậy n = 0.

b) Ta có :

n + 3 chia hết cho n - 1

=> n - 1 + 4 chia hết cho n - 1 (1)

Mà n - 1 chia hết cho n - 1 (2)

Từ (1) và (2) suy ra :

4 chia hết cho n - 1

=> n - 1 \(\in\) Ư(4) = {1; 2; 4}

Với n - 1 = 1 => n = 2

Với n - 1 = 2 => n = 3

Với n - 1 = 4 => n = 5

Vây n \(\in\) {2; 3; 5}.

T-I-C-K mình nha các bạn ~~ Please !!!