Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
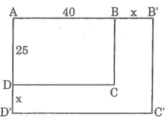
Sau khi tăng kích thước của mỗi chiều, ta được hình chữ nhật A’B’C’D’ có chiều dài A’B’ = (40 + x) cm, chiều rộng B’C’ = (25 + x) cm.
Các giá trị tương ứng của P:
| x | 0 | 1 | 1,5 | 2,5 | 3,5 |
| P = 4x + 130 | 130 | 134 | 136 | 140 | 144 |
Sau khi tăng kích thước của mỗi chiều, ta được hình chữ nhật A’B’C’D’ có chiều dài A’B’ = (40 + x) cm, chiều rộng B’C’ = (25 + x) cm.
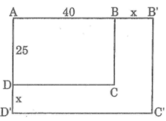
Diện tích hình chữ nhật mới:
S = (40 + x)(25 + x) = 1000 + 65x + x 2
S không phải là hàm số bậc nhất đối với x vì có bậc của biến số x là bậc hai.
Chu vi hình chữ nhật mới:
P = 2.[(40 + x) + (25 + x)] = 4x + 130
P là hàm số bậc nhất đối với x có hệ số a = 4, hệ số b = 130.
- Gọi hình chữ nhật ban đầu ABCD có kích thước AB = 30cm; BC = 20cm.
- Sau khi bớt các kích thước của hình chữ nhật đi x (cm), ta có hình chữ nhật mới là A'B'C'D' có:
A'B' = 30 – x
B'C' = 20 – x
Gọi y là chu vi của hình chữ nhật A'B'C'D', ta có:
y = 2[(30 - x) + (20 - x)]
=> y = 2(50 - 2x)
=> y = -4x + 100 (cm)
Khi bớt mỗi kích thước x (cm) thì được một hình chữ nhật có các kích thước
là 20 – x (cm) và 30 – x (cm).
Khi đó chu vi của hình chữ nhật là y=2(20–x+30–x)y=2(20–x+30–x)
hay y=100–4x
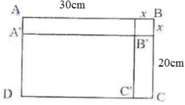
- Gọi hình chữ nhật ban đầu ABCD có kích thước AB = 30cm; BC = 20cm.
- Sau khi bớt các kích thước của hình chữ nhật đi x (cm), ta có hình chữ nhật mới là A'B'C'D' có:
A'B' = 30 – x
B'C' = 20 – x
Gọi y là chu vi của hình chữ nhật A'B'C'D', ta có:
y = 2[(30 - x) + (20 - x)]
=> y = 2(50 - 2x)
=> y = -4x + 100 (cm)
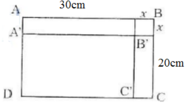
- Gọi hình chữ nhật ban đầu ABCD có kích thước AB = 30cm; BC = 20cm.
- Sau khi bớt các kích thước của hình chữ nhật đi x (cm), ta có hình chữ nhật mới là A'B'C'D' có:
A'B' = 30 – x
B'C' = 20 – x
Gọi y là chu vi của hình chữ nhật A'B'C'D', ta có:
y = 2[(30 - x) + (20 - x)]
=> y = 2(50 - 2x)
=> y = -4x + 100 (cm)
Gọi hình chữ nhật ban đầu là ABCDABCD có các cạnh AB=30cm,BC=20cmAB=30cm,BC=20cm.
Sau khi bớt mỗi cạnh của hình chữ nhật đi x(cm)x(cm), ta được hình chữ nhật mới là A′B′C′DA′B′C′D có các cạnh
A′B′=30−x(cm)A′B′=30−x(cm)
B′C′=20−x(cm)B′C′=20−x(cm)
Với yy là chu vi của hình chữ nhật A'B'C'D, ta có: y=2[(30−x)+(20−x)]y=2[(30−x)+(20−x)]
Rút gọn được y=−4x+100y=−4x+100.
Gọi hình chữ nhật ban đầu là có các cạnh .
Sau khi bớt mỗi cạnh của hình chữ nhật đi , ta được hình chữ nhật mới là có các cạnh
Với là chu vi của hình chữ nhật A'B'C'D, ta có:
Rút gọn được .
a: \(S=\left(30-x\right)\left(40-x\right)\)
\(=\left(x-30\right)\left(x-40\right)=x^2-70x+1200\)
=>S không là hàm số bậc nhất đối với x
\(P=2\left[30-x+40-x\right]=2\left(70-2x\right)=-4x+140\)
=>P là hàm số bậc nhất đối với x
b: Khi x=0 thì \(P=-4\cdot0+140=140\)
Khi x=1 thì \(P=140-4=136\)
Khi x=2 thì \(P=140-8=132\)
Khi x=3 thì \(P=140-12=128\)
Khi x=4 thì P=140-4*4=124
em cảm ơnn😻