Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Sửa câu c: DE // BE thành DE // BC nhé
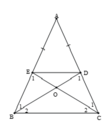
| GT | △ABC cân tại A. D BD ∩ ED = { O } |
KL | a, DB = EC b, △OBC cân; △ODE cân c, DE // BE |
Bài giải:
a, Vì △ABC cân tại A (gt) => AB = AC
Xét △BAD và △CAE
Có: AB = AC (cmt)
BAC là góc chung
AD = AE (gt)
=> △BAD = △CAE (c.g.c)
=> DB = CE (2 cạnh tương ứng)
b, Vì △BAD = △CAE (cmt)
=> ABD = ACE (2 góc tương ứng) và ADB = CEA (2 góc tương ứng)
Ta có: CEA + CEB = 180o (2 góc kề bù)
ADB + BDC = 180o (2 góc kề bù)
Mà ADB = CEA (cmt)
=> CEB = BDC
Lại có: AB = AE + EB
AC = AD + DC
Mà AB = AC (gt) ; AD = AE (gt)
=> EB = DC
Xét △BOE và △COD
Có: OBE = OCD (cmt)
BE = CD (cmt)
BEO = CDO (cmt)
=> △BOE = △COD (g.c.g)
=> OB = OC (2 cạnh tương ứng) và OE = OD (2 cạnh tương ứng)
Xét △OED có: OE = OD (cmt) => △OED cân tại O
Xét △OBC có: OB = OC (cmt) => △OBC cân tại O
c, Xét △AOD có: AE = AD (gt) => △AOD cân tại A => AED = (180o - EAD) : 2 (1)
Vì △ABC cân tại A (gt) => ABC = (180o - BAC) : 2 (2)
Từ (1) và (2) => AED = ABC
Mà 2 góc này nằm ở vị trí đồng vị
=> ED // BC (dhnb)

a) Xét △ABD và △ACE có:
AB = AC (gt)
\(\widehat{A}\) chung
AD = AE (gt)
\(\Rightarrow\)△ABD = △ACE (c.g.c)
\(\Rightarrow\)DB = EC (cặp cạnh tương ứng)
b) Ta có :△ABD = △ACE
\(\Rightarrow\widehat{B_1}=\widehat{C_1}\) (cặp góc tương ứng)
Mà \(\widehat{ABC}=\widehat{ACB}\) ( △ABC cân tại đỉnh A)
\(\Rightarrow\widehat{ABC}-\widehat{B_1}=\widehat{ACB}-\widehat{C_1}\)
\(\Rightarrow\widehat{OBC}=\widehat{OCB}\)
\(\Rightarrow\)△OBC cân tại đỉnh O
\(\Rightarrow\)OB = OC
Ta có: DB = EC (cmt)
OB = OC
\(\Rightarrow\)DB - OB = EC - OC
\(\Rightarrow\)OE = OD
\(\Rightarrow\)△ODE cân đỉnh O (ĐPCM)
c) △OBC cân tại đỉnh O
\(\Rightarrow\)\(\widehat{OCB}=\frac{180^o-\widehat{BOC}}{2}\)
△ODE cân tại đỉnh O
\(\Rightarrow\widehat{DEO}=\frac{180^o-\widehat{DOE}}{2}\)
Mà \(\widehat{BOC}=\widehat{DOE}\)(đối đỉnh)
\(\Rightarrow\widehat{DEO}=\widehat{OCB}\)
Vì 2 góc này nằm ở vị trí so le trong
\(\Rightarrow\)DE // BC (ĐPCM)

a) Ta có : \(AB=AC\) (do \(\Delta ABC\) cân tại A - gt)
Lại có :\(\left\{{}\begin{matrix}AB=AE+EB\\AC=AD+DC\end{matrix}\right.\)
Mà : \(AD=AE\left(gt\right)\)
Do đó : \(DB=EC\left(đpcm\right)\)
b) Xét \(\Delta ADB\) và \(\Delta AEC\)có :
\(AB=AC\left(gt\right)\)
\(\widehat{A}:chung\)
\(AE=AD\left(gt\right)\)
=> \(\Delta ADB\) = \(\Delta AEC\) (c.g.c)
=> \(EC=BD\) (2 cạnh tương ứng)
Xét \(\Delta EBC\) và \(\Delta DBC\)có :
\(EB=DC\) (cmt - câu a)
\(\widehat{EBC}=\widehat{DCB}\) (do tam giác ABC cân - gt)
\(BC:chung\)
=> \(\Delta EBC=\Delta DBC\) (c.g.c)
=> \(\widehat{ECB}=\widehat{DBC}\) (2 góc tương ứng)
Xét \(\Delta OBC\) có :
\(\widehat{OBC}=\widehat{OCB}\) [ \(\widehat{ECB}=\widehat{DBC}\) (cmt)]
=> \(\Delta OBC\) cân tại O
Xét \(\Delta EBD\) và \(\Delta DEC\) có :
\(EB=DC\left(cmt\right)\)
\(ED:chung\)
\(DB=EC\left(cmt\right)\)
=> \(\Delta EBD\) = \(\Delta DEC\) (c.c.c)
=> \(\widehat{EDB}=\widehat{DEC}\) (2 góc tương ứng)
=> \(\Delta ODE\) cân tại O

a: Xét ΔADB và ΔAEC có
AD=AE
góc BAD chung
AB=AC
Do đó: ΔABD=ΔACE
Suy ra: BD=CE
b: Xét ΔEBC và ΔDCB có
EB=DC
EC=DB
BC chung
Do đó: ΔEBC=ΔDCB
Suy ra: \(\widehat{OCB}=\widehat{OBC}\)
hay ΔOBC cân tại O
c: Xét ΔABC có AE/AB=AD/AC
nên DE//BC
 AC; E
AC; E 


a) Xét ΔABD và ΔACE có:
AB=ACAB=AC (do ΔABC cân đỉnh A)
ˆA^ : góc chung
AD=AE (giả thiết)
⇒ΔABD=ΔACE (c.g.c)
⇒DB=EC (hai cạnh tương ứng)
b) ΔABD=ΔACE⇒ˆB1=ˆC1 (hai góc tương ứng)
Mà ˆABC=ˆACB (do ΔABC cân đỉnh A)
⇒ˆABC−ˆB1=ˆACB−ˆC1
⇒ˆOBC=ˆOCB
⇒ΔOBC cân đỉnh O (đpcm)