Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a.
\(1-4x^2=\left(1-2x\right)\left(1+2x\right)\)
b.
\(8-27x^3=\left(2\right)^3-\left(3x\right)^3=\left(2-3x\right)\left(4+6x+9x^2\right)\)
c.
\(27+27x+9x^2+x^3=x^3+3.x^2.3+3.3^2.x+3^3\)
\(=\left(x+3\right)^3\)
d.
\(2x^3+4x^2+2x=2x\left(x^2+2x+1\right)=2x\left(x+1\right)^2\)
e.
\(x^2-y^2-5x+5y=\left(x-y\right)\left(x+y\right)-5\left(x-y\right)\)
\(=\left(x-y\right)\left(x+y-5\right)\)
f.
\(x^2-6x+9-y^2=\left(x-3\right)^2-y^2=\left(x-3-y\right)\left(x-3+y\right)\)

a)4(18 - 5x) - 12(3x - 7) = 15(2x - 16) - 6(x + 14)
<=>72 - 20x - 36x +84 = 30x - 240 - 6x 84
<=> -80x = -480
<=> x = 6
b) 5(3x+5)-4(2x-3) =5x+3(2x+12)+1
<=> 15x + 25 - 8x + 12 = 5x + 6x + 36 + 1
<=> 15x + 25 - 8x + 12 - 5x - 6x - 36 - 1 = 0
<=> -4x = 0
<=> x = 0
c) 2(5x-8)-3(4x-5)=4(3x-4)+11
= 10x - 16 - 12x + 15 = 12x - 16 + 11
= -14x = -4
= x =\(\frac{2}{7}\)
d) 5x-3{4x-2[4x-3(5x-2)]}=182
= 5x - 3 . [4x - 2(4x - 15x + 6)]
= 5x - 3 . (4x - 8x + 30x - 12)
= 5x - 12x + 24x - 90x + 36
= -73x + 36 = 182
=> -73x = 182 - 36 = 146
=> x = 146 : (-73) = -2
~Hok tốt~

\(a,\frac{30x^3}{11y^2}.\frac{121y^5}{25x}\)
\(=>\frac{30x^3.121y^5}{11y^2.25x}=\frac{6x^2.11y^3}{5}=\frac{66x^2.y^3}{5}\)
\(b,\frac{24y^5}{7x^2}.\frac{-21x}{12y^3}\)
\(=>\frac{24y^5.\left(-21\right)x}{7x^2.12y^3}=\frac{2y^2.\left(-3\right)}{x}=-\frac{6y^2}{x}\)
\(c,\left(\frac{-18y^3}{25x^4}\right).\left(\frac{-15x^2}{9y^3}\right)\)
\(=>\frac{-18y^3.\left(-15\right)x^2}{25x^4.9y^3}=\frac{-2.\left(-3\right)}{5x^2}=\frac{6}{5x^2}\)
\(d,\frac{3x^2}{2y}.\frac{1}{4y}.\frac{5}{3y}\)
\(=>\frac{3x^2.1.5}{2y.4y.3y}=\frac{15x^2}{24y^3}=\frac{5x^2}{8y^3}\)
\(e,\frac{2x}{3}.\frac{x+1}{2x}\)
\(=>\frac{2x\left(x+1\right)}{3.2x}=\frac{x+1}{3}\)
\(g,\frac{5-x}{x-3}.\frac{2}{3}.\frac{x}{4}\)
\(=>\frac{2x\left(5-x\right)}{3.4\left(x-3\right)}=\frac{10x-2x^2}{12\left(x-3\right)}=\frac{10x-2x^2}{12x-9}\)

a) 3x2 – 7x + 2
\(=3x^2-6x-x+2\)
\(=\left(3x^2-6x\right)-\left(x-2\right)\)
\(=3x\left(x-2\right)-\left(x-2\right)\)
\(=\left(x-2\right)\left(3x-1\right)\)
b) a(x2 + 1) – x(a2 + 1)
\(=ax^2+a-\left(a^2x+x\right)\)
\(=a\left(x^2+1\right)-x\left(a^2+1\right)\)
.......?
a) Ta có: \(3x^2-7x+2\)
\(=3x^2-6x-x+2\)
\(=3x\left(x-2\right)-\left(x-2\right)\)
\(=\left(x-2\right)\left(3x-1\right)\)
b) Ta có: \(a\left(x^2+1\right)-x\left(a^2+1\right)\)
\(=x^2a+a-a^2x-x\)
\(=\left(x^2a-a^2x\right)+\left(a-x\right)\)
\(=xa\left(x-a\right)-\left(x-a\right)\)
\(=\left(x-a\right)\left(xa-1\right)\)
c) Ta có: \(\left(x+2\right)\left(x+3\right)\left(x+4\right)\left(x+5\right)-24\)
\(=\left(x^2+7x+10\right)\left(x^2+7x+12\right)-24\)
\(=\left(x^2+7x\right)^2+22\left(x^2+7x\right)+120-24\)
\(=\left(x^2+7x\right)^2+22\left(x^2+7x\right)+96\)
\(=\left(x^2+7x\right)^2+16\left(x^2+7x\right)+6\left(x^2+7x\right)+96\)
\(=\left(x^2+7x\right)\left(x^2+7x+16\right)+6\left(x^2+7x+16\right)\)
\(=\left(x^2+7x+16\right)\left(x^2+7x+6\right)\)
\(=\left(x^2+7x+16\right)\left(x+1\right)\left(x+6\right)\)
d) Ta có: \(\left(a+1\right)\left(a+3\right)\left(a+5\right)\left(a+7\right)+15\)
\(=\left(a^2+8a+7\right)\left(a^2+8a+15\right)+15\)
\(=\left(a^2+8a\right)^2+22\left(a^2+8a\right)+105+15\)
\(=\left(a^2+8a\right)^2+22\left(a^2+8a\right)+120\)
\(=\left(a^2+8a\right)^2+12\left(a^2+8a\right)+10\left(a^2+8a\right)+120\)
\(=\left(a^2+8a\right)\left(a^2+8a+12\right)+10\left(a^2+8a+12\right)\)
\(=\left(a^2+8a+12\right)\left(a^2+8a+10\right)\)
\(=\left(a+2\right)\left(a+6\right)\left(a^2+8a+10\right)\)

b) \(x^2+6x+9=144\)
\(\Leftrightarrow\left(x+3\right)^2=12^2\)
\(\Leftrightarrow\left[{}\begin{matrix}x+3=12\\x+3=-12\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=9\\x=-15\end{matrix}\right.\)
b, Ta có : \(x^2+6x+9=144\)
=> \(\left(x+3\right)^2=12^2\)
=> \(\left[{}\begin{matrix}x+3=12\\x+3=-12\end{matrix}\right.\)
=> \(\left[{}\begin{matrix}x=9\\x=-15\end{matrix}\right.\)
Vậy phương trình có tập nghiệm là \(S=\left\{9,-15\right\}\)
c, Ta có : \(\frac{2-x}{2016}-1=\frac{1-x}{2017}-\frac{x}{2018}\)
=> \(\frac{2-x}{2016}-1=\frac{1-x}{2017}+\frac{-x}{2018}\)
=> \(\frac{2-x}{2016}+1=\frac{1-x}{2017}+1+\frac{-x}{2018}+1\)
=> \(\frac{2-x}{2016}+\frac{2016}{2016}=\frac{1-x}{2017}+\frac{2017}{2017}+\frac{-x}{2018}+\frac{2018}{2018}\)
=> \(\frac{2018-x}{2016}=\frac{2018-x}{2017}+\frac{2018-x}{2018}\)
=> \(\frac{2018-x}{2016}-\frac{2018-x}{2017}-\frac{2018-x}{2018}=0\)
=> \(\left(2018-x\right)\left(\frac{1}{2016}-\frac{1}{2017}-\frac{1}{2018}\right)=0\)
=> \(2018-x=0\)
=> \(x=2018\)
Vậy phương trình có tập nghiệm là \(S=\left\{2018\right\}\)

Bài 3
a) x² + 10x + 25
= x² + 2.x.5 + 5²
= (x + 5)²
b) 8x - 16 - x²
= -(x² - 8x + 16)
= -(x² - 2.x.4 + 4²)
= -(x - 4)²
c) x³ + 3x² + 3x + 1
= x³ + 3.x².1 + 3.x.1² + 1³
= (x + 1)³
d) (x + y)² - 9x²
= (x + y)² - (3x)²
= (x + y - 3x)(x + y + 3x)
= (y - 2x)(4x + y)
e) (x + 5)² - (2x - 1)²
= (x + 5 - 2x + 1)(x + 5 + 2x - 1)
= (6 - x)(3x + 4)
Bài 4
a) x² - 9 = 0
x² = 9
x = 3 hoặc x = -3
b) (x - 4)² - 36 = 0
(x - 4 - 6)(x - 4 + 6) = 0
(x - 10)(x + 2) = 0
x - 10 = 0 hoặc x + 2 = 0
*) x - 10 = 0
x = 10
*) x + 2 = 0
x = -2
Vậy x = -2; x = 10
c) x² - 10x = -25
x² - 10x + 25 = 0
(x - 5)² = 0
x - 5 = 0
x = 5
d) x² + 5x + 6 = 0
x² + 2x + 3x + 6 = 0
(x² + 2x) + (3x + 6) = 0
x(x + 2) + 3(x + 2) = 0
(x + 2)(x + 3) = 0
x + 2 = 0 hoặc x + 3 = 0
*) x + 2 = 0
x = -2
*) x + 3 = 0
x = -3
Vậy x = -3; x = -2

\(a,=10x^3-5x^2+5x\\ b,=x^3+27\\ c,=\dfrac{5}{2}xy-1-\dfrac{1}{2}y\\ d,=\left(2x^3-10x^2-11x^2+55x+12x-60\right):\left(x-5\right)\\ =\left[2x^2\left(x-5\right)-11x\left(x-5\right)+12\left(x-5\right)\right]:\left(x-5\right)\\ =2x^2-11x+12\)
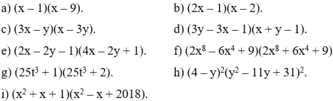
Bài 1:
a) \(25x^4-\frac{1}{9}y^2\)
\(=\left(5x^2\right)^2-\left(\frac{1}{3}y\right)^2\)
\(=\left(5x^2-\frac{1}{3}y\right).\left(5x^2+\frac{1}{3}y\right)\)
c) \(x^2-3\)
\(=x^2-\left(\sqrt{3}\right)^2\)
\(=\left(x-\sqrt{3}\right).\left(x+\sqrt{3}\right)\)
d) \(x^2-16x^2y^2z^2\)
\(=x^2-\left(4xyz\right)^2\)
\(=\left(x-4xyz\right).\left(x+4xyz\right)\)
Chúc bạn học tốt!
b, \(\left(x+5\right)y^2-\left(x+5\right)3\)
\(=\left(x+5\right)\left(y^2.3\right)\)