Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Áp dụng công thức: p = d.h, ta có: 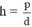
- Độ sâu của tàu ngầm ở thời điểm trước khi nổi lên:
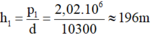
- Độ sâu của tàu ngầm ở thời điểm sau khi nổi lên:
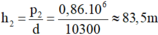

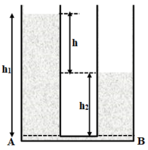
Giả sử ta đổ xăng vào nhánh bên trái, khi đó chiều cao của cột xăng là h1, nước bên trong ống bên phải dâng lên có độ cao là h2.
Ta có: h = 18mm = 0,018m; d1 = 7000N/m3; d2 = 10300 N/m3.
Xét hai điểm A và B trong hai nhánh nằm trong cùng một mặt phẳng ngang trùng với mặt phân cách giữa xăng và nước biển.
Ta có: pA = pB mà pA = d1.h1; pB = d2.h2;
Suy ra: d1.h1 = d2.h2;
Theo hình vẽ thì h2 = h1 – h, do đó:
d1.h1 = d2.(h1 – h) = d2.h1 – d2.h
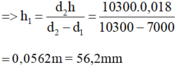

a, Tàu đàn nổi lên vì áp suất sau nhỏ hơn áp suất trước, chứng tỏ độ chênh lệch độ sâu với mặt nước biển đang giảm
b, Độ sâu của tàu ở hai thời điểm:
\(h_1=\dfrac{p_1}{d}=\dfrac{2,02.10^6}{10300}=196,11(m)\)
\(h_2=\dfrac{p_2}{d}=\dfrac{0,86.10^6}{10300}=83,5(m)\)

Áp dụng công thức: p = d.h ⇒ h = p/d
Độ sâu của tàu ngầm ở thời điểm trước khi nổi lên:
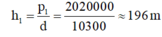
Độ sâu của tàu ngầm ở thời điểm sau khi nổi lên:
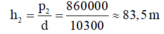
⇒ Đáp án A

a) Ta có: p 1 > p 2 ( d o 2020000 > 860000 ) ⇔ d h 1 > d h 2 ⇔ h 1 > h 2 b) Tàu ngầm đang ngoi lên
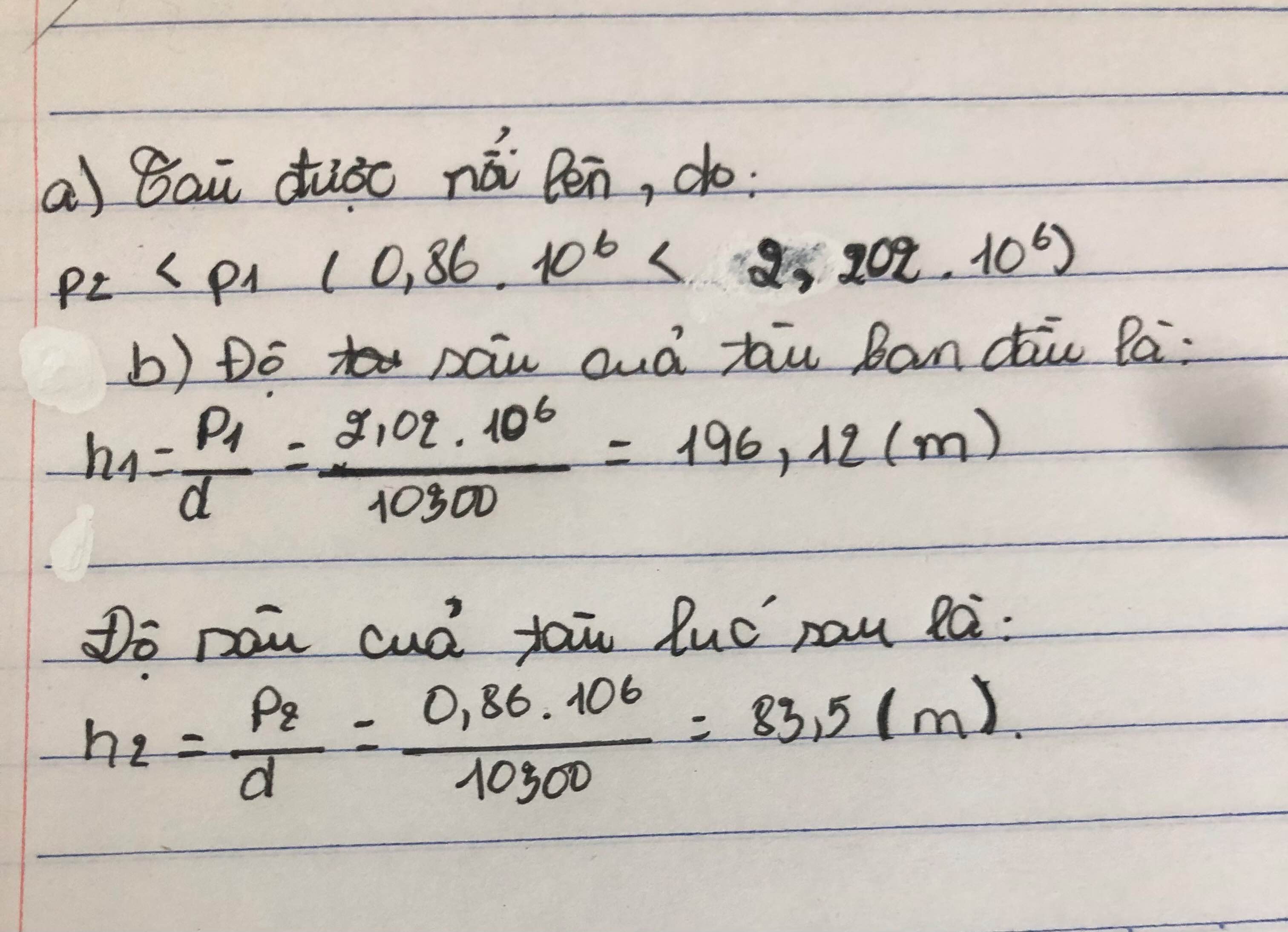
Bài 1:
a) Tàu đang nổi lên. Ta khẳng định được như vậy do áp suất chất lỏng được viết bởi công thức: \(p=d.h\Rightarrow\) \(p\) và \(h\) tỉ lệ thuận với nhau theo hệ số tỉ lệ \(d\). Mà \(d\) ở 2 địa điểm trên bằng nhau => Ở áp suất \(2,02.10^6N\)/\(m^2\) thì độ sâu sẽ sâu hơn ở áp suất \(0,86.10^6N\)/\(m^2\).
b) Áp dụng công thức tinh áp suất chất lỏng: \(p=d.h\Rightarrow h=\frac{p}{d}=\frac{p}{10300}\)
Gọi \(h_1;h_2\) lần lượt là độ sâu của tàu ở áp suất \(2,02.10^6N\)/\(m^2\) và ở áp suất \(0,86.10^6N\)/\(m^2\).
=> \(h_1=\frac{2,02.10^6}{10300}\approx196,1\left(m\right);h_2=\frac{0,86.10^6}{10300}\approx83,5\left(m\right)\)
Bài 2: Tóm tắt
\(h=18cm\)
\(d_2=10300N\)/\(m^3\)
\(d_1=7000N\)/\(m^3\)
______________
\(h_1=?\)
Giải
Ta có: \(p_A=p_B\Rightarrow d_2.h_2=d_1.h_1\Rightarrow d_2.\left(h_1-h\right)=d_1.h_1\Rightarrow10300h_1-7000h_1=10300h\)
\(\Rightarrow3300h_1=10300.18\Rightarrow h_1\approx56,19\left(cm\right)\)