Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

1/
a/ Ta có AB < BC (5cm < 6cm)
=> \(\widehat{ACB}< \widehat{A}\)(quan hệ giữa góc và cạnh đối diện trong tam giác)
Mà \(\widehat{ACB}=\widehat{ABC}\)(\(\Delta ABC\)cân tại A)
=> \(\widehat{ABC}< \widehat{A}\)
b/ \(\Delta ADB\)và \(\Delta ADC\)có: AB = AC (\(\Delta ABC\)cân tại A)
\(\widehat{BAD}=\widehat{DAC}\)(AD là tia phân giác \(\widehat{BAC}\))
Cạnh AD chung
=> \(\Delta ADB\)= \(\Delta ADC\)(c. g. c) (đpcm)
c/ Ta có \(\Delta ABC\)cân tại A
=> Đường cao AD cũng là đường trung tuyến của \(\Delta ABC\)
và G là giao điểm của hai đường trung tuyến AD và BE của \(\Delta ABC\)
=> CF là đường trung tuyến thứ ba của \(\Delta ABC\)
=> F là trung điểm AB (đpcm)
d/ Ta có G là giao điểm của ba đường trung tuyến AD, BE và CF của \(\Delta ABC\)
=> G là trọng tâm \(\Delta ABC\)
và D là trung điểm BC (vì AD là đường trung tuyến của \(\Delta ABC\))
=> \(BD=DC=\frac{BC}{2}=\frac{6}{2}=3\)(cm)
Áp dụng định lý Pitago vào \(\Delta ADB\)vuông tại D, ta có: AD = 4cm (tự tính)
=> \(AG=\frac{2}{3}AD=\frac{2}{3}.4=\frac{8}{3}\)(cm)
Áp dụng định lý Pitago vào \(\Delta ADC\)vuông tại D, ta có:
\(BG=\sqrt{BD^2+GD^2}\)
=> \(BG=\sqrt{3^2+\left(\frac{8}{3}\right)^2}\)
=> \(BG=\sqrt{9+\frac{64}{9}}\)
=> \(BG=\sqrt{\frac{145}{9}}\)
=> BG \(\approx\)4, 01 (cm)

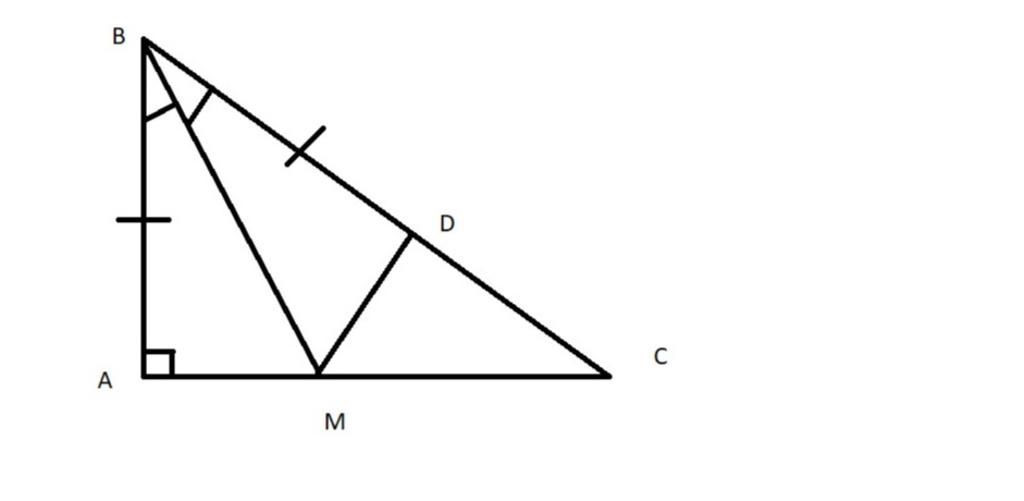
a: Xét ΔABM và ΔDBM có
BA=BD
\(\widehat{ABM}=\widehat{DBM}\)
BM chung
Do đó: ΔABM=ΔDBM
b: Ta có: ΔBAM=ΔBDM
nên \(\widehat{BAM}=\widehat{BDM}=90^0\)
hay MD\(\perp\)BC
c: Ta có: MA=MD
mà MD<MC
nên MA<MC

a: \(\widehat{ABC}=90^0-40^0=50^0>\widehat{ACB}\)
nên AC>AB
b: \(BC=\sqrt{6^2+10^2}=2\sqrt{34}\left(cm\right)\)
c: Xét ΔBAD vuông tại A và ΔBED vuông tại E có
BD chung
\(\widehat{ABD}=\widehat{EBD}\)
DO đó:ΔBAD=ΔBED
Suy ra: BA=BE
hay ΔABE cân tại B

a, Xét \(\Delta ABC\)VUÔNG tại A
Áp dụng định lý pitago ta có:
\(BC^2=AB^2+AC^2\)
\(\Rightarrow AB^2=BC^2-AC^2\)
\(\Rightarrow AB^2=10^2-6^2\)
\(\Rightarrow AB^2=100-36\)
\(\Rightarrow AB^2=64\)
\(\Rightarrow AB=\sqrt{64}=8\)
VẬY AB=8 cm
b, Xét \(\Delta ABD\)và \(\Delta HBD\)CÓ:
\(\widehat{BAD}=\widehat{BHD}=90độ\)
\(\widehat{ABD}=\widehat{HBD}\)(do BD là tia phân giác của \(\widehat{B}\))
BD là cạnh chung
\(\Rightarrow\Delta ABD=\Delta HBD\)(ch-gn)
\(\Rightarrow AD=HD\)(2 CẠNH TƯƠNG ỨNG)
c,Do \(\Delta ABD=\Delta HBD\left(câub\right)\)
\(\Rightarrow\widehat{BDA}=\widehat{BDH}\)(2 góc tương ứng)
lại có \(\widehat{ADK}=\widehat{HDC}\)(đối đỉnh)
\(\Rightarrow\widehat{BDA}+\widehat{ADK}=\widehat{BDH}+\widehat{HDC}\)
\(\Rightarrow\widehat{BDK}=\widehat{BDC}\)
Xét \(\Delta KBD\) VÀ \(\Delta CBD\)CÓ:
\(\widehat{ABD}=\widehat{CBD}\)(Do BD là tia phân giác của \(\widehat{B}\))
BD là cạnh chung
\(\widehat{BDK}=\widehat{BDC}\left(cmt\right)\)
Do đó \(\Delta KBD=\Delta CBD\left(g-c-g\right)\)
\(\Rightarrow BK=BC\)(2 CẠNH TƯƠNG ỨNG)
\(\Rightarrow\Delta KBC\) cân tại B


a)Xét △ABM và △△ DBM , ta có :
AB=BD(gt)
ˆABM^ == ˆDBM^ ( vì BM là tia phân giác của ˆABC^ )
BM là chung
⇒ △△ ABM= △△ DBM(c−g−c)
b)Ta có : ˆBAM^ == ˆBDM (( vì △ ABM= △ DBM)
Mà ˆBAM^ =90o(=90) ( vì △ ABC vuông tại A)
⇒⇒ ˆBDM=90o
⇒MD⇒ ⊥⊥ BC
c) Vì MD⊥⊥ BC(cmt)
⇒ ˆMDC^ =90o=90
⇒ △ MDC vuông tại D
⇒MC>MD(ch>cgv)
Mà MD=MA( vì △ABM=△ DBM)
⇒MC>MA


a)
Xét tam giác ABM và tam giác ACM có :
góc B = góc C (gt )
AB=AC ( gt )
góc A1 = góc A2 (gt )
suy ra : tam giác ABM = tam giác ACM ( g - c -g )
b )
ta có : tam giác ABM = tam giác ACM suy ra : BM = CM = BC : 2 = 3 (cm )
Theo định lí pitago trong tam giác vuông ABM có :
AB2 = AM2 + BM2
SUY RA : AM2 = AB2 - BM2
AM2 = 52 - 32
AM = căn bậc 2 của 16 = 4 (cm )
c )
Do D nằm giữa 2 điểm M và C nên ta có :
MD + DC = MC
suy ra : MC > MD
Đúng thì nha bạn