Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đặt AI = x (cm) , (x>0) , IC = y (cm) , (y>0)
Ta có : \(2y^2=18,2015\Rightarrow y=\sqrt{\frac{18,2015^2}{2}}\)
Mặt khác : \(x^2+DI^2=AD^2=14,2014^2\) ; \(y^2+DI^2=CD^2=18,2015^2\)
\(\Rightarrow y^2-x^2=18,2015^2-14,2014^2\Rightarrow x=\sqrt{y^2-18,2015^2+14,2014^2}\)
Từ đó dễ dàng giải tiếp bài toán.

Kẻ đường cao BE \(\Rightarrow BE=12\)
Pitago tam giác vuông BDE:
\(DE=\sqrt{BD^2-BE^2}=9\left(cm\right)\)
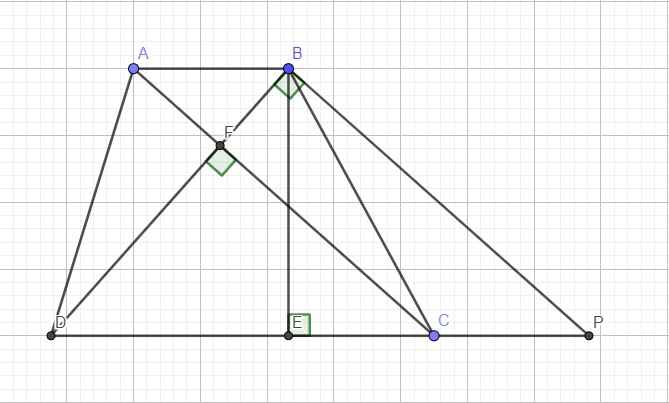
Qua B kẻ đường thẳng song song AC cắt CD kéo dài tại P
Do \(AC\perp BD\Rightarrow BP\perp BD\) hay tam giác BPD vuông tại B
Mặt khác \(\left\{{}\begin{matrix}AB||CD\\AC||BP\end{matrix}\right.\) \(\Rightarrow ABPC\) là hbh
\(\Rightarrow AB=CP\Rightarrow AB+CD=CP+CD=DP\)
Hệ thức lượng tam giác vuông BPD:
\(BD^2=DE.DP\Rightarrow DP=\dfrac{BD^2}{DE}=25\left(cm\right)\)
\(S_{ABCD}=\dfrac{1}{2}BE.\left(AB+CD\right)=\dfrac{1}{2}BE.DP=\dfrac{1}{2}.9.25=112,5\left(cm^2\right)\)
bạn vẽ hình chưa?
chưa ạ><