Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B
Giả sử chiều dài của hình chữ nhật giáp với bờ sông
Gọi x , y (m) lần lượt là chiều rộng, chiều dài của hình chữ nhật.
Theo giả thiết, ta có: 2 x + y = 2400 ⇔ y = 2400 − 2 x
Suy ra:
S = x y = 2400 − 2 x x = 720000 − 2 x − 600 2 ≤ 720000
Dấu "=" xảy ra ⇔ x = 600 . Vậy diện tích lớn nhất là 720000 m 2

Gọi x là chiều rộng bãi cỏ thì chiều dài bãi cỏ sẽ là 1000 - 2x
Khi đó diện tích bãi cỏ là:
S = x( 1000 - 2x ) = 1000x - 2 x 2 .
Ta có S'(x) = 1000 - 4x = 0 nên x = 250
Vậy max S = S (250) = 125000 m 2
Đáp án D

Đáp án C
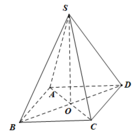
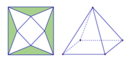
S A = 1 − x 2 2 2 + 1 4 = 1 − x 2 + x 2 2 A O = x 2 2 , S O = S A 2 − A O 2 = 1 − x 2 + x 2 − x 2 2 = 1 − x 2 2 V = 1 3 S O . S A B C D = 1 3 x 2 1 − x 2 2 f ( x ) = x 2 1 − x 2 2 , x ∈ 0 ; 1 f ' ( x ) = 4 x − 5 2 x 2 4 1 − x 2 2 f ' ( x ) = 0 ⇔ x = 0 ( L ) x = 2 2 5







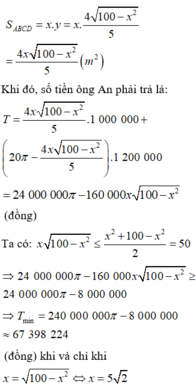

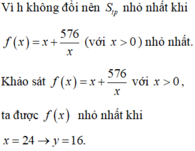

Đáp án D
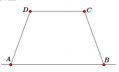
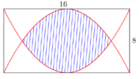
Gọi H, K lần lượt là hình chiếu của D, C trên AB
Vì ABCD là hình thang cân ⇒ AH = BK;CD = HK
Đặt A H = x ⇒ A B = H K + 2 A H = 2 x + 4 và D H = 16 - x 2
Diện tích hình thang cân ABCD là
S A B C D = 1 2 D H . A B + C D = x + 4 16 - x 2 = f x
Xét hàm số f x = x + 4 16 - x 2 trên ( 0 ; 4 ] → m a x ( 0 ; 4 ] f x = 12 3 . Vậy S m a x = 12 3