Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi từ số của phân số cần tìm là: a.
Gọi mẫu số của phân số cần tìm là:b
Theo đề ta có:
\(a=b-8\)
\(\Rightarrow\frac{a}{b}=\frac{a}{a+8}\)
Ta lại có:
\(\frac{a+3}{a+8-3}=\frac{5}{6}\)\(\Rightarrow\frac{a+3}{a+5}=\frac{5}{6}\)
\(\Rightarrow\frac{a+5-2}{a+5}=\frac{5}{6}\Rightarrow\frac{a+5}{a+5}-\frac{2}{a+5}=\frac{5}{6}\)
\(=1-\frac{2}{a+5}=\frac{5}{6}\)
\(\frac{2}{a+5}=1-\frac{5}{6}=\frac{1}{6}\)
\(a+5=\frac{2}{\frac{1}{6}}=12\)
\(a=12-5=7\)
\(=>b=7+8=15\)
Vậy phân số ban đầu là: \(\frac{7}{15}\)

a: Xét ΔHBA vuông tại H và ΔABC vuông tại A có
góc B chung
=>ΔHBA đồng dạng với ΔABC
b: BC=căn 12^2+16^2=20cm
AH=12*16/20=9,6cm

a: Xét ΔHBA vuông tại H và ΔABC vuông tại A có
góc B chung
=>ΔHBA đồng dạng với ΔABC
b: BC=căn AB^2+AC^2=20cm
AH=12*16/20=9,6cm

Mình làm câu hình thôi. Hôm qua đang làm thì máy sập và..
(Hình xấu quá, sorry)
a/ Xét \(\Delta AHB\)và \(\Delta BCD\)có:
\(\widehat{AHB}=\widehat{BCD}=90^0\left(gt\right)\)
\(\widehat{ABH}=\widehat{BDC}\)(Vì AB//DC, tính chất hình chữ nhật, so le trong)
\(\Rightarrow\Delta ABH~\Delta BDC\left(g.g\right)\)
b/ Xét \(\Delta AHD\)và \(\Delta ADB\)có:
\(\widehat{AHD}=\widehat{DAB}=90^0\left(gt\right)\)
\(\widehat{ADB}:chung\)
\(\Rightarrow\Delta ADH~\Delta BDA\left(g.g\right)\)
\(\Rightarrow\frac{AD}{DB}=\frac{DH}{AD}\)
\(\Rightarrow AD.AD=DH.DB\)
\(\Rightarrow AD^2=DH.DB\)
c/ Ta có: \(BC=AD=9\left(cm\right)\)(tính chất hình chữ nhật)
Xét \(\Delta ABD\)vuông tại \(A\)có:
\(AD^2+AB^2=BD^2\left(pytago\right)\)
\(9^2+12^2=BD^2\)
\(81+144=BD^2\)
\(225=BD^2\)
\(\Rightarrow BD=\sqrt{225}=15\left(cm\right)\)
Ta có: \(\frac{AD}{DB}=\frac{DH}{AD}\left(cmt\right)\Leftrightarrow\frac{9}{15}=\frac{DH}{9}\Rightarrow DH=\frac{9.9}{15}=5,4\left(cm\right)\)
Ta lại có: \(AH=BD-DH=15-5,4=9,6\left(cm\right)\)

Gọi tử số của phân số ban đầu là a, theo bài ra ta có:
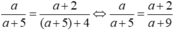
(Điều kiện: a ≠ - 5;a ≠ - 9 )
a(a + 9) = (a + 2)(a + 5)
⇔ a 2 + 9 a = a 2 + 7 a + 10
⇔ 2a = 10 ⇔ a = 5 (Thỏa mãn)
Vậy phân số cần tìm là: 5/10

