Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bài 3:
Đặt \(a=m^2-4\)
\(a)\) Đồ thị hàm số \(y=\left(m^2-4\right)x-5\)nghịch biến
\(\Leftrightarrow a< 0\)
\(\Leftrightarrow m^2-4< 0\)
\(\Leftrightarrow m^2< 4\)
\(\Leftrightarrow-\sqrt{4}< m< \sqrt{4}\)
\(\Leftrightarrow-2< m< 2\)
Vậy với \(-2< m< 2\)thì hàm số nghịch biến
\(b)\) Đồ thị hàm số \(y=\left(m^2-4\right)x-5\)đồng biến \(\forall x>0\)
\(\Leftrightarrow a>0\)
\(\Leftrightarrow m^2-4>0\)
\(\Leftrightarrow m^2>4\)
\(\Leftrightarrow\orbr{\begin{cases}m>2\\m< -2\end{cases}}\)
Vậy với \(\orbr{\begin{cases}m>2\\m< -2\end{cases}}\)thì hàm số đồng biến \(\forall x>0\)

a)
đường thẳng (d1) song song với đường thẳng (d2) khi :
a = a' và b khác b'
suy ra :
\(m-1=3\) \(\Leftrightarrow m=4\)
vậy đường thẳng (d1) song song với đường thẳng (d2) khi m = 4

a, y là hàm số bậc nhất khi \(2-m\ne0\Leftrightarrow m\ne2\)
b , y đồng biến khi 2 - m > 0 => m < 2
y nghịch biến khi 2 - m < 0 => m > 2
c, (d) // y=4-x khi
\(\hept{\begin{cases}2-m=4\\m-1\ne-x\end{cases}}\Leftrightarrow\hept{\begin{cases}m=-2\\m\ne-x+1\end{cases}}\Leftrightarrow m=-2\)
👍👍✔✔✔

a) (d) // (d') khi m - 3 = 1
m = 1 + 3
m = 4
Vậy m = 4 thì (d) // (d')
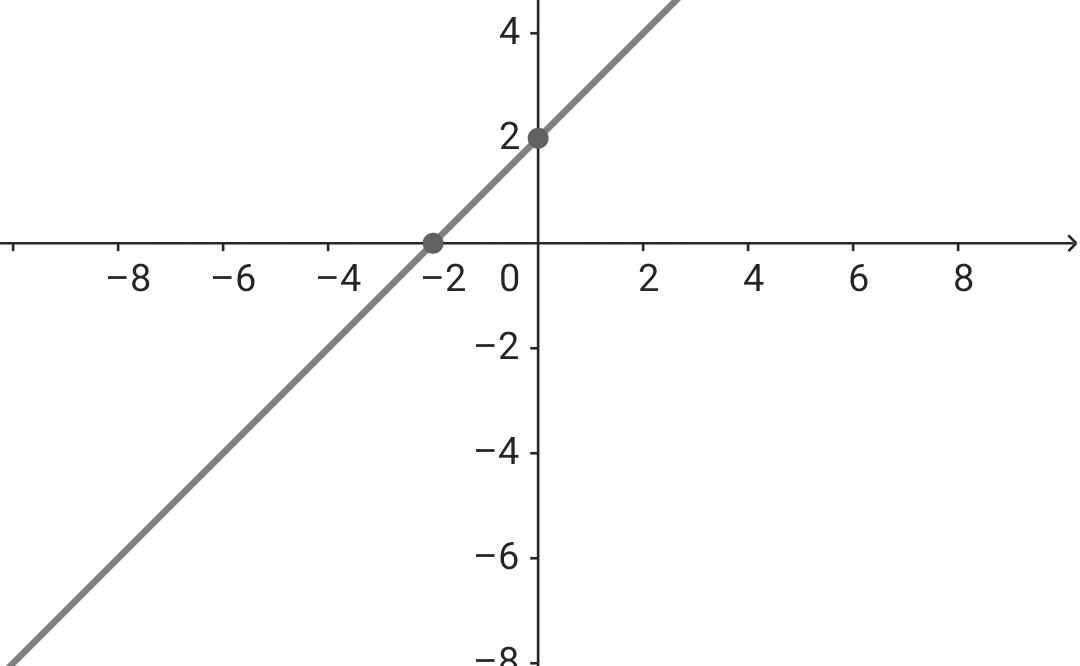
b) Với m = 4 ⇒ (d): y = x + 2
Đồ thị:

1. a) Để hs trên là hs bậc nhất khi và chỉ khi a>0 --> 3+2k>0 --> k >\(\frac{-3}{2}\)
b) Vì đths cắt trục tung tại điểm có tung độ = 5 --> x=0, y=5
Thay y=5 và x=0 vào hs và tìm k
2. a) Tự vẽ
b) Hệ số góc k=\(\frac{-a}{b}=\frac{-2}{4}=\frac{-1}{2}\)
c) Phương trình hoành độ giao điểm là:\(2x+4=-x-2\)(tìm x rồi thay x vào 1 trong 2 pt --> tính y) (x=-2; y=0)
3. Vì 3 đg thẳng đồng quy -->d1 giao d2 giao d3 tại 1 điểm (giao kí hiệu là chữ U ngược)
Tính tọa độ giao điểm của d1 và d2 --> x=2;y=1
Điểm (2;1) thuộc d3 --> Thay x=2 và y=1 vào d3 -->m=3

a) (d) // (d') khi m - 3 = 1
m = 1 + 3
m = 4
Vậy m = 4 thì (d) // (d')
b) Với m = 4 ⇒ (d): y = x + 2
Đồ thị:
