N
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
LT
3
13 tháng 12 2015
a,Có số số hạng là:
(1001-1)+1=1001(số)
Tổng là:
(1001+1) x 1001:2=501501
b,Có số số hạng là:
(999-1) :2+1=500(số)
Tổng là:
(999+1) x 500:2=250000
c,tương tự câu b
tick nha tí nữa thi xong Anh cấp trương
LH
2
AH
Akai Haruma
Giáo viên
9 tháng 12 2023
Lời giải:
$A=[(-1)+5]+[(-9)+13]+....+[(-41)+45]$
$=4+4+4+....+4$
Số lần xuất hiện của 4 là: $[(45-1):4+1]:2=6$
$A=4\times 6=24$
-------------------------
$B=(1-2-3+4)+(5-6-7+8)+....+(997-998-999+1000)$
$=0+0+.....+0=0$
17 tháng 10 2021
\(a,S_3=-2-2-...-2\)
Tổng có \(\left[\left(2003-1\right):2+1\right]:2=501\left(số.hạng\right)\)
\(\Rightarrow S_3=501\cdot\left(-2\right)=-1002\)
\(b,S_4=\left(-1001+1001\right)+\left(-1000+1000\right)+...+\left(-1+1\right)+1002\\ S_4=1002\)
17 tháng 10 2021
a: \(S_3=1+\left(-3\right)+5+\left(-7\right)+...+2001+\left(-2003\right)\)
=(-2)+(-2)+...+(-2)
=-2004
GN
GV Nguyễn Trần Thành Đạt
Giáo viên
4 tháng 12 2023
C = 1 + (-3) + 5 + (-7) +...+ 2001 + (-2003)
C= (1 - 2003) + (2001 - 3) + (5 - 1999) + (1997 - 7) +...+ (1001 - 1003)
C= -2002 + 1998 - 1994 + 1990 +....-2
C= (-4) + (-4) +....+ (-4) - 2 (250 cặp (-4) )
C= 250 x (-4) - 2
C= -1000 - 2 = -1002
GN
GV Nguyễn Trần Thành Đạt
Giáo viên
4 tháng 12 2023
D = (-1001) + (-1000) + (-999) +...+ 1001 + 1002
D= (1001 - 1001) + (1000 - 1000) +...+ (1-1) + 0 + 1002
D= 0 + 0 +... + 0 + 0 + 1002
D= 1002
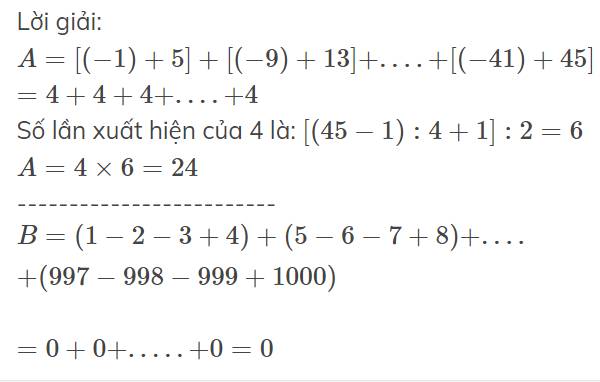
a) \(A=1.2+2.3+3.4+...+999.1000\)
\(3A=1.2.3+2.3.\left(4-1\right)+3.4.\left(5-2\right)+...+999.1000.\left(1001-998\right)\)
\(=1.2.3+2.3.4-1.2.3+3.4.5-2.3.4+...+999.1000.1001-998.999.1000\)
\(=999.1000.1001\)
\(A=\frac{999.1000.1001}{3}\)
b) \(B=1.3+3.5+5.7+...+999.1001\)
\(6B=1.3.6+3.5.\left(7-1\right)+5.7.\left(9-3\right)+...+999.1001.\left(1003-997\right)\)
\(=1.3.6+3.5.7-1.3.5+5.7.9-3.5.7+...+999.1001.1003-997.999.1003\)
\(=999.1001.1003+1.3\)
\(B=\frac{999.1001.1003+1.3}{6}\)