K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
AD
1
13 tháng 11 2023
bạn ghi rõ nội dung, yêu cầu đề của bài đó ra cho mình nha
22 tháng 10 2018
Cấm đăng câu hỏi linh tinh !!!!!!!!!!!!!!!!!!!!!!!!!
NV
22 tháng 10 2018
I. Nội qui tham gia "Giúp tôi giải toán"
1. Không đưa câu hỏi linh tinh lên diễn đàn, chỉ đưa các bài mà mình không giải được hoặc các câu hỏi hay lên diễn đàn;
2. Không trả lời linh tinh, không phù hợp với nội dung câu hỏi trên diễn đàn.
3. Không "Đúng" vào các câu trả lời linh tinh nhằm gian lận điểm hỏi đáp.
Các bạn vi phạm 3 điều trên sẽ bị giáo viên của Online Math trừ hết điểm hỏi đáp, có thể bị khóa tài khoản hoặc bị cấm vĩnh viễn không đăng nhập vào trang web.
Đọc đi để nhớ và lần sau đừng đăng câu hỏi linh tinh như thế nữa.
AH
Akai Haruma
Giáo viên
14 tháng 7 2020
Lời giải:
a) Ta thấy:
$\Delta'=m^2-(m^2-9)=9>0$ với mọi $m$ nên PT luôn có 2 nghiệm phân biệt với mọi $m$
b)
Ở phần $a$ ta đã chỉ ra pt luôn có 2 nghiệm pb với mọi $m$. Áp dụng định lý Vi-et với $x_1,x_2$ là nghiệm của pt ta có: \(\left\{\begin{matrix} x_1+x_2=2m\\ x_1x_2=m^2-9\end{matrix}\right.\)
Khi đó:
\(x_2^2=18-x_1(x_2+x_1)\)
\(\Leftrightarrow x_2^2+x_1(x_2+x_1)=18\)
\(\Leftrightarrow x_1^2+x_2^2+x_1x_2=18\)
\(\Leftrightarrow (x_1+x_2)^2-x_1x_2=18\)
\(\Leftrightarrow (2m)^2-(m^2-9)=18\)
\(\Leftrightarrow 3m^2=27\Leftrightarrow m^2=9\Leftrightarrow m=\pm 3\)
c) Theo hệ thức Viet đã chỉ ra ở phần b:
\(\Rightarrow \left\{\begin{matrix} (x_1+x_2)^2=4m^2\\ 4x_1x_2=4m^2-36\end{matrix}\right.\)
\(\Rightarrow (x_1+x_2)^2-4x_1x_2=36\)
\(\Leftrightarrow (x_1-x_2)^2=36\Leftrightarrow |x_1-x_2|=6\) (đây chính là hệ thức liên hệ giữa $x_1,x_2$ mà không phụ thuộc vào $m$)
30 tháng 4 2020
Hùng Nguyễn làm giúp e đi anh hùng ới ơi 
e h ngu cái hpt quá r
NV
Nguyễn Việt Lâm
Giáo viên
13 tháng 7 2020
\(A=\frac{a\sqrt{a}-3}{\left(\sqrt{a}+1\right)\left(\sqrt{a}-3\right)}-\frac{\left(2\sqrt{a}-6\right)\left(\sqrt{a}-3\right)}{\left(\sqrt{a}+1\right)\left(\sqrt{a}-3\right)}-\frac{\left(\sqrt{a}+3\right)\left(\sqrt{a}+1\right)}{\left(\sqrt{a}+1\right)\left(\sqrt{a}-3\right)}\)
\(=\frac{a\sqrt{a}-3a+8\sqrt{a}-24}{\left(\sqrt{a}+1\right)\left(\sqrt{a}-3\right)}=\frac{\left(\sqrt{a}-3\right)\left(a+8\right)}{\left(\sqrt{a}+1\right)\left(\sqrt{a}-3\right)}=\frac{a+8}{\sqrt{a}-3}\)
\(\Delta'=n^2-n^2+9=9>0;\forall n\)
\(\Rightarrow\) Pt luôn có 2 nghiệm pb
Do \(x_2\) là nghiệm của pt nên:
\(x^2_2-2nx_2+n^2-9=0\Rightarrow x_2^2=2nx_2-n^2+9\)
Thay vào bài toán:
\(2nx_2-n^2+9=7-x_1x_2-2nx_1\)
\(\Leftrightarrow2n\left(x_1+x_2\right)+x_1x_2-n^2+2=0\)
\(\Leftrightarrow4n^2+n^2-9-n^2+2=0\)
\(\Rightarrow n^2=\frac{7}{4}\Rightarrow n=...\)
Bạn kiểm tra lại tính toán
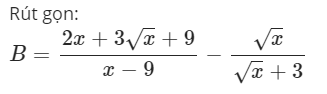
\(B=\dfrac{2x+3\sqrt{x}+9}{x-9}-\dfrac{\sqrt{x}}{\sqrt{x}+3}\)
\(\Rightarrow B=\dfrac{2x+3\sqrt{x}+9}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}-\dfrac{\sqrt{x}\left(\sqrt{x}-3\right)}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}\)
\(\Rightarrow B=\dfrac{2x+3\sqrt{x}+9}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}-\dfrac{x-3\sqrt{x}}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}\)
\(\Rightarrow B=\dfrac{2x+3\sqrt{x}+9-x+3\sqrt{x}}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}\)
\(\Rightarrow B=\dfrac{x+6\sqrt{x}+9}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}\)
\(\Rightarrow B=\dfrac{\left(\sqrt{x}+3\right)^2}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}\)
\(\Rightarrow B=\dfrac{\sqrt{x}+3}{\sqrt{x}-3}\)
\(\dfrac{2x+3\sqrt{x}+9-\sqrt{x}\left(\sqrt{x}-3\right)}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}=\dfrac{\left(\sqrt{x}+3\right)^2}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}=\dfrac{\sqrt{x}+3}{\sqrt{x}-3}\)