K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
TT
0
DP
1
12 tháng 9 2020
Bài 1. Điền kí hiệu ( ∈,⊂, ∉) thích hợp vào ô vuông
– 3 ∉ N – 3 ∈ Z -3 ∈ Q
-2/3 ∉ Z -2/3 ∈ Q N ⊂ Z ⊂ Q
Bài 2 trang 7. Trong các phân số sau, những phân số nào biểu diễn số hữu tỉ 3/-4
bài 3
hD Giải: a) x= 2/-7 = -22/7;y = -3/11= -21/77
Vì -22 < -21 và 77> 0 nên x <y
b)
Vì -216 < -213 và 300 > 0 nên y < x
c) x = -0,75 = -75/100 = -3/4; y = -3/4
Vậy x=y
Bài 4. So sánh số hữu tỉ a/b ( a,b ∈ Z, b # 0) với số 0 khi a, b cùng dấu và khi a, b khác dấu
HD giải: Với a, b ∈ Z, b> 0
– Khi a , b cùng dấu thì a/b > 0
– Khi a,b khác dấu thì a/b < 0
Tổng quát: Số hữu tỉ a/b ( a,b ∈ Z, b # 0) dương nếu a,b cùng dấu, âm nếu a, b khác dấu, bằng 0 nếu a = 0
TD
2
TH
18 tháng 11 2016
Giải:
∆AHB và ∆KBH có
AH=KH ( gt )
=
BH cạnh chung .
Nên ∆AHB=∆KBH(c.g.c)
Suy ra: =
Vậy BH là tia phân giác của góc B.
Tương tự ∆AHC =∆KHC ( c . g . c )
Suy ra: =
Vậy CH là tia phân giác của góc C
p/s: Very làm biếng open sách so copy mạng =]]]
NK
4
4 tháng 3 2021
1)
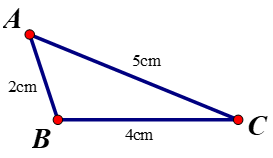
Dựa vào hình vẽ, ta có:
Góc đối diện cạnh BC là Â
Góc đối diện cạnh AC là B̂
Góc đối diện cạnh AB là Ĉ
Mà: Trong một tam giác, góc đối diện với cạnh lớn hơn là góc lớn hơn
Tam giác ABC có AB = 2cm, BC = 4cm, AC = 5cm ⇒ AB < BC < CA ⇒ Ĉ < Â < B̂.
2)heo định lý tổng ba góc trong tam giác ABC, ta có:
Cạnh đối diện góc B là AC
Cạnh đối diện góc C là AB
Cạnh đối diện góc A là BC
Trong một tam giác, cạnh đối diện với góc lớn hơn là cạnh lớn hơn.
Vì 450 < 550 < 800 hay B̂ < Ĉ < Â ⇒ AC < AB < BC.
Kiến thức áp dụng
+ Định lí 2: Trong một tam giác, cạnh đối diện với góc lớn hơn là cạnh lớn hơn.
+ Định lý tổng ba góc trong tam giác: Trong một tam giác, tổng ba góc bằng 180º.
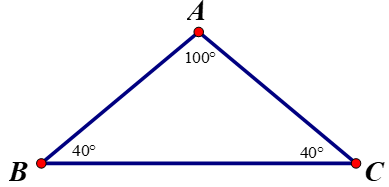
3 a) Trong tam giác ABC có góc A là góc tù nên cạnh đối diện với góc A là cạnh lớn nhất.
Cạnh đối diện với góc A là BC nên suy ra cạnh BC lớn nhất.
b) Tam giác ABC là tam giác tù vì có 1 góc A tù.
Áp dụng định lý tổng ba góc trong tam giác ABC ta có
4) Trong một tam giác ta luôn có:
+ Góc đối diện với cạnh lớn hơn là góc lớn hơn
⇒ góc đối diện với cạnh nhỏ nhất là góc nhỏ nhất.
+ Góc nhỏ nhất luôn là góc nhọn.
(Giả sử tồn tại tam giác có góc nhỏ nhất không phải góc nhọn
⇒ Góc nhỏ nhất ≥ 90º ⇒ cả ba góc ≥ 90º ⇒ tổng ba góc trong tam giác ≥ 90º.3 = 270º.
5) + Trong ∆BCD có góc C tù (gt) nên góc C lớn nhất ⇒ BD lớn nhất (vì BD là cạnh đối diện với góc C) ⇒ BD > CD (1).
+ Áp dụng định lý góc ngoài trong tam giác BCD ta có :
nên góc ABD cũng là góc tù.
Trong ∆ABD có góc B tù (cmt) nên góc B lớn nhất ⇒ AD lớn nhất (vì AD là cạnh đối diện với góc B) ⇒ AD > BD
(2).
Từ (1) và (2) suy ra AD > BD > CD.
Vậy Hạnh đi xa nhất, Trang đi gần nhất.
6)Vì D nằm giữa A và C (giả thiết)
⇒ AC = AD + DC = AD + BC (DC = BC theo đề bài)
⇒ AC > BC
Mà trong tam giác ABC :
Góc đối diện cạnh AC là góc B
Góc đối diện cạnh BC là góc A
Ta lại có: AC > BC (cmt)
⇒ B̂ > Â (theo định lí 1)
Hay  < B̂.
Vậy kết luận c) là đúng.
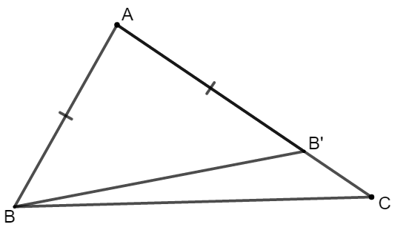
7)
a) Trên tia AC, ta có : AC > AB mà AB = AB’ ⇒ AC > AB’ ⇒ B’ nằm giữa A và C.
⇒ tia B’B nằm giữa hai tia BA và BC.
b) ∆ABB’ có AB = AB’ nên ∆ABB’ cân tại A.
c) Vì góc AB'B là góc ngoài tại B’ của ∆BB’C
PG
25 tháng 11 2018
a) 108 . 28 = (10.2)8 = 208
b) 108 : 28 = (10:2)8 = 58
c) 254 . 28 = 58 . 28 = 108
d) 158 . 94 = 158 . 38 = 458
e) 272 : 253 = (33)2 : (52)3 = 33.2 : 52.3 = 36 : 56 = 
HT
2
8 tháng 7 2017
a) Ta có: \(2^{27}=(2^{3})^{9}=8^{9}\)
\(3^{18}=(3^{2})^{9}=9^{9}\)
b) Vì 8< 9 nên \(8^{9}<9^{9}\)
Vậy theo câu a, ta được \(3^{18}\) < \(2^{27}\)
!Ai học rùi thì giúp tui với.Nhớ giúp cho hẳn hoi đấy
nên hai tỉ số trên không lập thành tỉ lệ thức
NH
2
HT
16 tháng 9 2015
Bài 44:
a, 1,2 : 3,24 = \(\frac{1,2}{3,24}=\frac{120}{324}=\frac{10}{27}\)
b, \(2\frac{1}{5}:\frac{3}{4}=3\frac{41}{45}=\frac{176}{45}\)
c,\(\frac{2}{7}:0,42=\frac{\frac{2}{7}}{0,42}=\frac{2}{7}.\frac{100}{42}=\frac{100}{147}\)
16 tháng 9 2015
vào đây nè:Chuyên trang lý thuyết tổng hợp các môn THPT bài nào cũng có
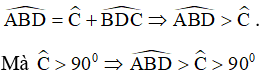
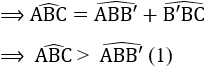
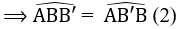
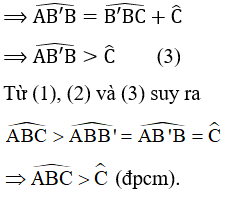
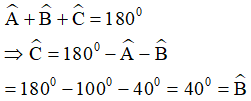
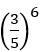
69 ) a) 8,5:3 = 2,8333... = 2,8(3)
b) 18,7 : 6 = 3,11666... = 3,11(6)
c) 58:11 = 5,272727... = 5,(27)
d) 14,2 : 3,33 = 4,264264264... = 4,(264)