
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



\(a,A=0,2\left(5x-1\right)-\dfrac{1}{2}\left(\dfrac{2}{3}x+4\right)+\dfrac{2}{3}\left(3-x\right)\)
\(=x-0,2-\dfrac{1}{3}x-2+2-\dfrac{2}{3}x\)
\(=\left(-0,2-2+2\right)+\left(x-\dfrac{1}{3}x-\dfrac{2}{3}x\right)\)
\(=-0,2\)
\(b,B=\left(x-2y\right)\left(x^2+2xy+4y^2\right)-\left(x^3-8y^3+10\right)\)
\(=x^3-8y^3-x^3+8y^3-10\)
\(=-10\)
\(c,C=4\left(x+1\right)^2+\left(2x-1\right)^2-8\left(x-1\right)\left(x+1\right)-4x\)
\(=4\left(x^2+2x+1\right)+\left(4x^2-4x+1\right)-8\left(x^2-1\right)-4x\)
\(=4x^2+8x+4+4x^2-4x+1-8x^2+8-4x\)
\(=13\)
a) \(A=0,2\left(5x-1\right)-\dfrac{1}{2}\left(\dfrac{2}{3}x+4\right)+\dfrac{2}{3}\left(3-x\right)\)
\(A=x-\dfrac{1}{5}-\dfrac{1}{3}x-2+2-\dfrac{2}{3}x\)
\(A=\left(x-\dfrac{1}{3}x-\dfrac{2}{3}x\right)-\left(\dfrac{1}{5}+2-2\right)\)
\(A=-\dfrac{1}{5}\)
Vậy: ...
b) \(B=\left(x-2y\right)\left(x^2+2xy+4y^2\right)-\left(x^3-8y^3+10\right)\)
\(B=\left[x^3-\left(2y\right)^3\right]-\left[x^3-\left(2y\right)^3\right]-10\)
\(B=-10\)
Vậy: ...
c) \(4\left(x+1\right)^2+\left(2x-1\right)^2-8\left(x+1\right)\left(x-1\right)-4x\)
\(=4\left(x^2+2x+4\right)+\left(4x^2-4x+1\right)-8\left(x^2-1\right)-4x\)
\(=4x^2+8x+4+4x^2-4x+1-8x^2+8-4x\)
\(=\left(4x^2+4x^2-8x^2\right)+\left(8x-4x-4x\right)+\left(4+1+8\right)\)
\(=13\)
Vậy:...



1: Xét tứ giác BHCK có
CH//BK
BH//CK
Do đó: BHCK là hình bình hành
Suy ra: Hai đường chéo BC và HK cắt nhau tại trung điểm của mỗi đường
mà M là trung điểm của BC
nên M là trung điểm của HK
2: Gọi giao điểm của IH và BC là O
Suy ra: IH\(\perp\)BC tại O và O là trung điểm của IH
Xét ΔHIK có
O là trung điểm của HI
M là trung điểm của HK
Do đó: OM là đường trung bình của ΔHIK
Suy ra: OM//IK
hay BC//IK
mà BC\(\perp\)IH
nên IH\(\perp\)IK
Xét ΔHOC vuông tại O và ΔIOC vuông tại O có
OC chung
HO=IO
Do đó: ΔHOC=ΔIOC
Suy ra: CH=CI
mà CH=BK
nên CI=BK
Xét tứ giác BCKI có IK//BC
nên BCKI là hình thang
mà CI=BK
nên BCKI là hình thang cân

a: Xét tứ giác ABDC có
M là trung điểm của BC
M là trung điểm của AD
Do đó: ABDC là hình bình hành
mà \(\widehat{BAC}=90^0\)
nên ABDC là hình chữ nhật

5:
a: Xét ΔABD vuông tại D và ΔACE vuông tại E có
góc A chung
=>ΔABD đồng dạng với ΔACE
b; ΔABD đồng dạng với ΔACE
=>AD/AE=AB/AC
=>AD/AB=AE/AC
Xét ΔADE và ΔABC có
AD/AB=AE/AC
góc DAE chung
=>ΔADE đồng dạng với ΔABC
c: ΔADE đồng dạng với ΔABC
=>S ADE/S ABC=(AD/AB)^2=1/4

a: Xét tứ giác AEHF có
\(\widehat{AEH}=\widehat{AFH}=\widehat{FAE}=90^0\)
Do đó: AEHF là hình chữ nhật
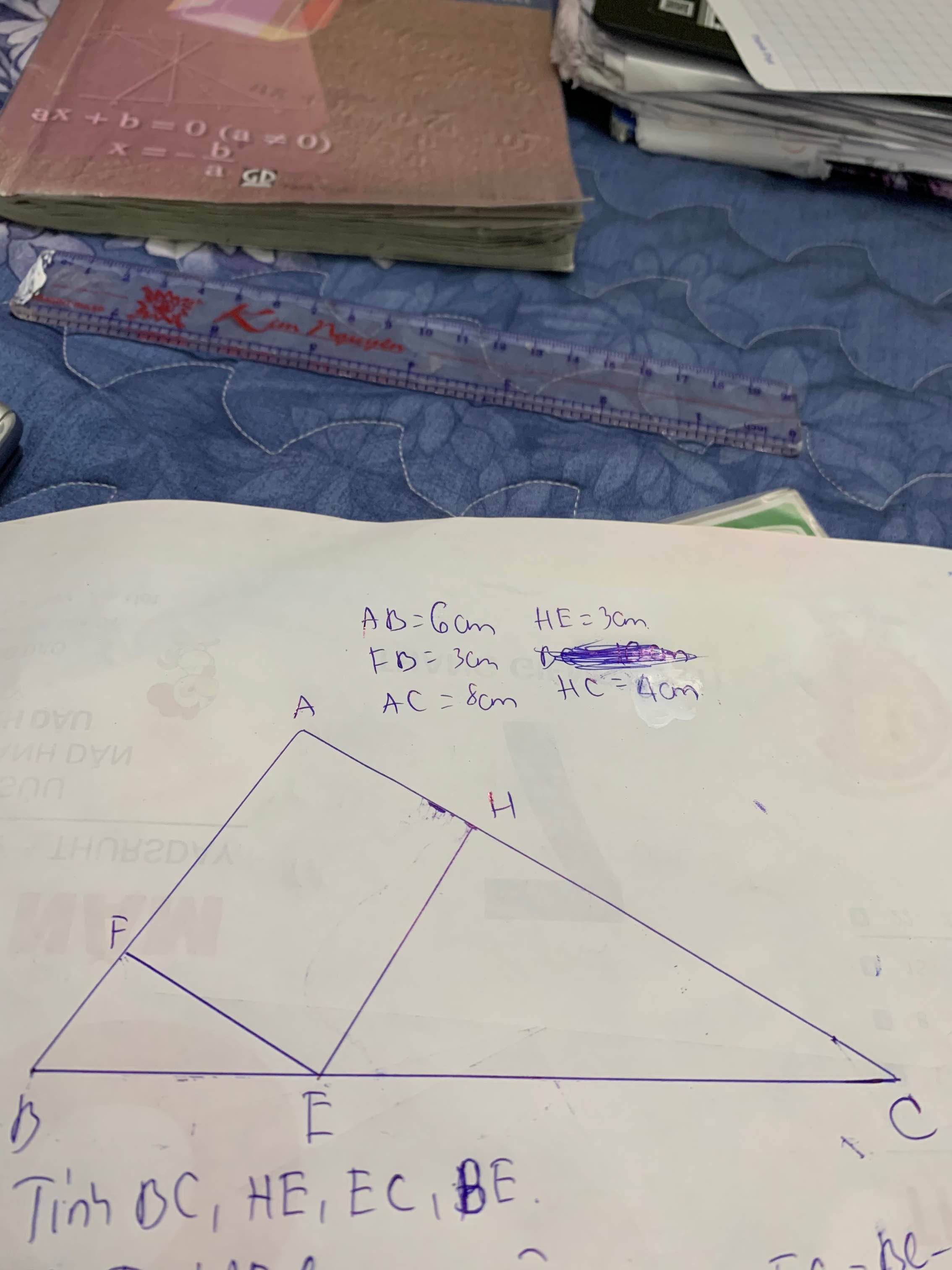

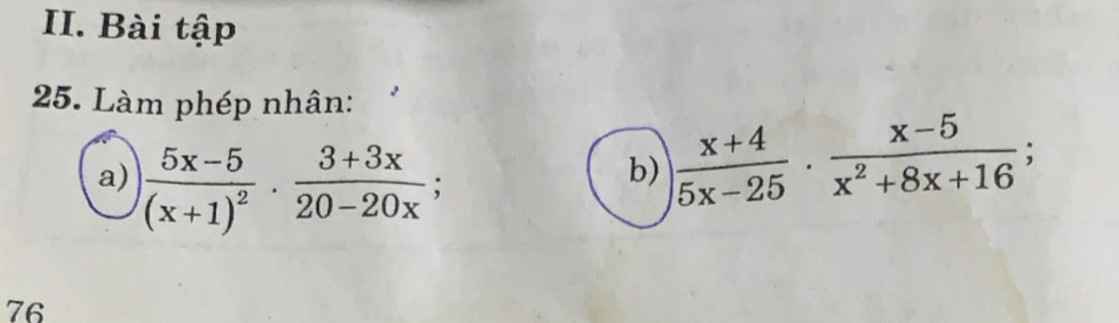
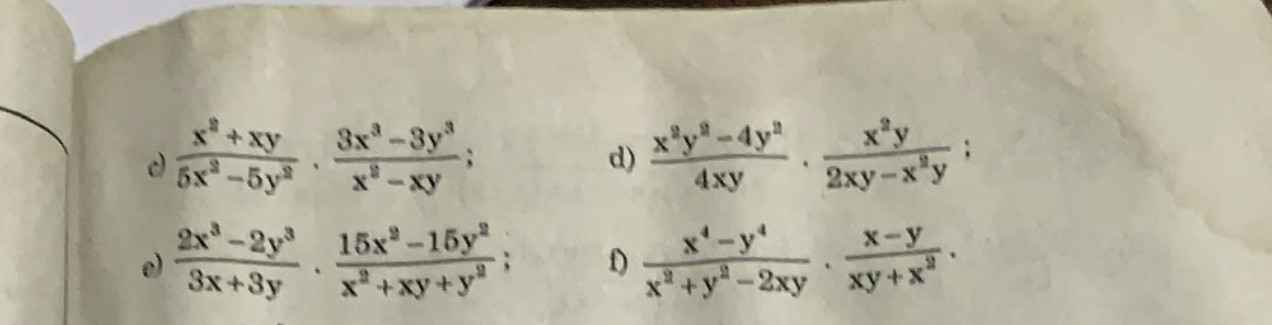

 giúp mình với ạ, mình cần gấp lắm ạ
giúp mình với ạ, mình cần gấp lắm ạ

\(P=\left[\dfrac{x\left(x-2\right)}{2\left(x^2+4\right)}-\dfrac{2x^2}{\left(2-x\right)\left(x^2+4\right)}\right]\cdot\dfrac{x^2-x-2}{x^2}\\ P=\dfrac{-x\left(x-2\right)^2-4x^2}{2\left(x^2+4\right)\left(2-x\right)}\cdot\dfrac{\left(x-2\right)\left(x+1\right)}{x^2}\\ P=\dfrac{x^3+4x}{2\left(x^2+4\right)\left(x-2\right)}\cdot\dfrac{\left(x-2\right)\left(x+1\right)}{x^2}\\ P=\dfrac{x\left(x^2+4\right)\left(x+1\right)}{2x^2\left(x^2+4\right)}=\dfrac{x+1}{2x}\)