K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
4 tháng 12 2021
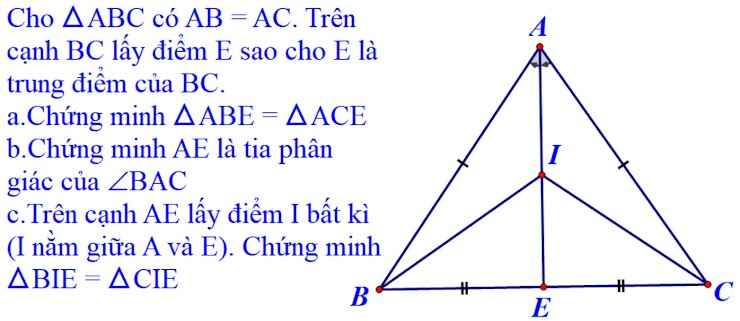
a) Xét tam giác ABE và tam giác ACE có:
+ AE chung.
+ AB = AC (gt).
+ BE = CE (E là trung điểm của BC).
=> Tam giác ABE = Tam giác ACE (c - c - c).
b) Xét tam giác ABC có: AB = AC (gt).
=> Tam giác ABC cân tại A.
Mà AE là đường trung tuyến (E là trung điểm của BC).
=> AE là phân giác ^BAC (Tính chất các đường trong tam giác cân).
c) Xét tam giác ABC cân tại A có:
AE là phân giác ^BAC (cmt).
=> AE là đường cao (Tính chất các đường trong tam giác cân).
=> AE \(\perp\) BC.
Xét tam giác BIE và tam giác CIE:
+ IE chung.
+ BE = CE (E là trung điểm của BC).
+ ^BEI = ^CEI ( = 90o).
=> Tam giác BIE = Tam giác CIE (c - g - c).
11 tháng 8 2018
| 7x - 10 | + 7x = 10
| 7x - 10 | = 10 - 7x
=> 7x - 10 thuộc { 10 - 7x; -10 + 7x }
+) 7x - 10 = 10 - 7x
7x + 7x = 10 + 10
14x = 20
x = 10/7
+) 7x - 10 = -10 + 7x
7x - 7x = -10 + 10
0x = 0
=> x = 0
Học tốt O.o
SM
11 tháng 8 2018
TH1 : x < 10/7
=> / 7x - 10 / +7x = 10 - 7x + 7x = 10 ( luôn đúng )
=> với mọi x < 10/7, ta luôn có / 7x - 10 / + 7x = 10
TH2 : x = 10/7
=> /7x - 10/ + 7x = 0 + 7x = 10
=> x = 10/ 7 ( thỏa mãn )
TH3 : x > 10/7
=> / 7x - 10 / + 7x = 7x - 10 + 7x = 10
=> 14 x = 10
=> x = 10/ 7 ( loại )
Vậy với mọi x < 10/7, biểu thức trên luôn đúng
25 tháng 12 2021
Bài 5:
Gọi số sách 7A,7B,7C,7D lần lượt là \(a,b,c,d\in \mathbb{N^*},sách\)
Áp dụng tc dtsbn:
\(\dfrac{a}{37}=\dfrac{b}{37}=\dfrac{c}{40}=\dfrac{d}{36}=\dfrac{c-d}{40-36}=\dfrac{12}{4}=3\\ \Rightarrow\left\{{}\begin{matrix}a=111\\b=111\\c=120\\d=108\end{matrix}\right.\)
Vậy ...
Bài 6:
Gọi cd, cr theo thứ tự là \(a,b>0;m\)
\(\Rightarrow a:b=5:4\Rightarrow\dfrac{a}{5}=\dfrac{b}{4}\)
Đặt \(\dfrac{a}{5}=\dfrac{b}{4}=k\Rightarrow a=5k;b=4k\)
Mà \(ab=500\Rightarrow20k^2=500\Rightarrow k^2=25\Rightarrow k=5\left(k>0\right)\)
\(\Rightarrow\left\{{}\begin{matrix}a=5\cdot5=25\\b=5\cdot4=20\end{matrix}\right.\\ \Rightarrow\text{Chu vi là }2\left(a+b\right)=2\left(25+20\right)=90\left(m\right)\)
TK
1
17 tháng 10 2021
Câu 3:
a: Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x}{3}=\dfrac{y}{2}=\dfrac{x+y}{3+2}=\dfrac{90}{5}=18\)
Do đó: x=54; y=36
15 tháng 1 2022
a: Xét ΔAMB và ΔAMC có
AM chung
\(\widehat{BAM}=\widehat{CAM}\)
AB=AC
Do đó: ΔAMB=ΔAMC
b: Ta có: ΔABC cân tại A
mà AM là đường phân giác
nên AM là đường trung trực
NT
0
NM
5
16 tháng 9 2021
\(2^{600}=\left(2^3\right)^{200}=8^{200}\)
\(3^{400}=\left(3^2\right)^{200}=9^{200}\)
VÌ \(8^{200}< 9^{200}\)
---> \(2^{600}< 3^{400}\)
XIN TIICK
16 tháng 9 2021
2 mũ 600 nhé mà a zai lớp 6 hỏi cái này làm gì
t i c k e nhé a zai :)
DM
1
AH
Akai Haruma
Giáo viên
12 tháng 8 2023
Lời giải:
a. Với $n$ nguyên khác -3, để $B$ nguyên thì:
$2n+9\vdots n+3$
$\Rightarrow 2(n+3)+3\vdots n+3$
$\Rightarrow 3\vdots n+3$
$\Rightarrow n+3\in\left\{\pm 1; \pm 3\right\}$
$\Rightarrow n\in\left\{-2; -4; 0; -6\right\}$
b.
$B=\frac{2n+9}{n+3}=\frac{2(n+3)+3}{n+3}=2+\frac{3}{n+3}$
Để $B_{\max}$ thì $\frac{3}{n+3}$ max
Điều này đạt được khi $n+3$ là số nguyên dương nhỏ nhất
Tức là $n+3=1$
$\Leftrightarrow n=-2$
c. Để $B$ min thì $\frac{3}{n+3}$ min
Điều này đạt được khi $n+3$ là số nguyên âm lớn nhất
Tức là $n+3=-1$
$\Leftrightarrow n=-4$
2 tháng 12 2021
ĐKXĐ : 2x \(\ge\)0 <=> x \(\ge\)0
| 7 + x | = 2x <=> \(\orbr{\begin{cases}7+x=2x\\7+x=-2x\end{cases}}\)
<=> \(\orbr{\begin{cases}x=7\\x=\frac{-7}{3}\end{cases}}\)( KTMĐK)
Vậy x = 7