K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
DM
1
AH
Akai Haruma
Giáo viên
12 tháng 8 2023
Lời giải:
a. Với $n$ nguyên khác -3, để $B$ nguyên thì:
$2n+9\vdots n+3$
$\Rightarrow 2(n+3)+3\vdots n+3$
$\Rightarrow 3\vdots n+3$
$\Rightarrow n+3\in\left\{\pm 1; \pm 3\right\}$
$\Rightarrow n\in\left\{-2; -4; 0; -6\right\}$
b.
$B=\frac{2n+9}{n+3}=\frac{2(n+3)+3}{n+3}=2+\frac{3}{n+3}$
Để $B_{\max}$ thì $\frac{3}{n+3}$ max
Điều này đạt được khi $n+3$ là số nguyên dương nhỏ nhất
Tức là $n+3=1$
$\Leftrightarrow n=-2$
c. Để $B$ min thì $\frac{3}{n+3}$ min
Điều này đạt được khi $n+3$ là số nguyên âm lớn nhất
Tức là $n+3=-1$
$\Leftrightarrow n=-4$
AH
Akai Haruma
Giáo viên
27 tháng 8 2023
Lời giải:
Đặt $\frac{a}{b}=\frac{c}{d}=k$
$\Rightarrow a=bk, c=dk$. Khi đó:
$\frac{a-b}{b}=\frac{bk-b}{b}=\frac{b(k-1)}{b}=k-1(1)$
$\frac{c-d}{d}=\frac{dk-d}{d}=\frac{d(k-1)}{d}=k-1(2)$
Từ $(1); (2)\Rightarrow \frac{a-b}{b}=\frac{c-d}{d}$
-------------------
$\frac{2a+3b}{2a-3b}=\frac{2bk+3b}{2bk-3b}=\frac{b(2k+3)}{b(2k-3)}=\frac{2k+3}{2k-3}(3)$
$\frac{2c+3d}{2c-3d}=\frac{2dk+3d}{2dk-3d}=\frac{d(2k+3)}{d(2k-3)}=\frac{2k+3}{2k-3}(4)$
Từ $(3); (4)\Rightarrow \frac{2a+3b}{2a-3b}=\frac{2c+3d}{2c-3d}$
VT
1
NM
1
17 tháng 11 2021
Bài 4
\(a,x:y=3:5\Rightarrow\dfrac{x}{3}=\dfrac{y}{5};y:z=4:5\Rightarrow\dfrac{y}{4}=\dfrac{z}{5}\\ \Rightarrow\dfrac{x}{12}=\dfrac{y}{20}=\dfrac{z}{25}=\dfrac{x+y+z}{12+20+25}=\dfrac{456}{57}=8\\ \Rightarrow\left\{{}\begin{matrix}x=96\\y=160\\z=200\end{matrix}\right.\)
\(b,a:b=2:3\Rightarrow\dfrac{a}{2}=\dfrac{b}{3};b:c=4:5\Rightarrow\dfrac{b}{4}=\dfrac{c}{5};c:d=6:7\Rightarrow\dfrac{c}{6}=\dfrac{d}{7}\\ \Rightarrow\dfrac{a}{8}=\dfrac{b}{12}=\dfrac{c}{15};\dfrac{c}{6}=\dfrac{d}{7}\\ \Rightarrow\dfrac{a}{16}=\dfrac{b}{24}=\dfrac{c}{30}=\dfrac{d}{35}=\dfrac{a+b+c+d}{16+24+30+35}=\dfrac{210}{105}=2\\ \Rightarrow\left\{{}\begin{matrix}a=32\\b=48\\c=60\\d=70\end{matrix}\right.\)
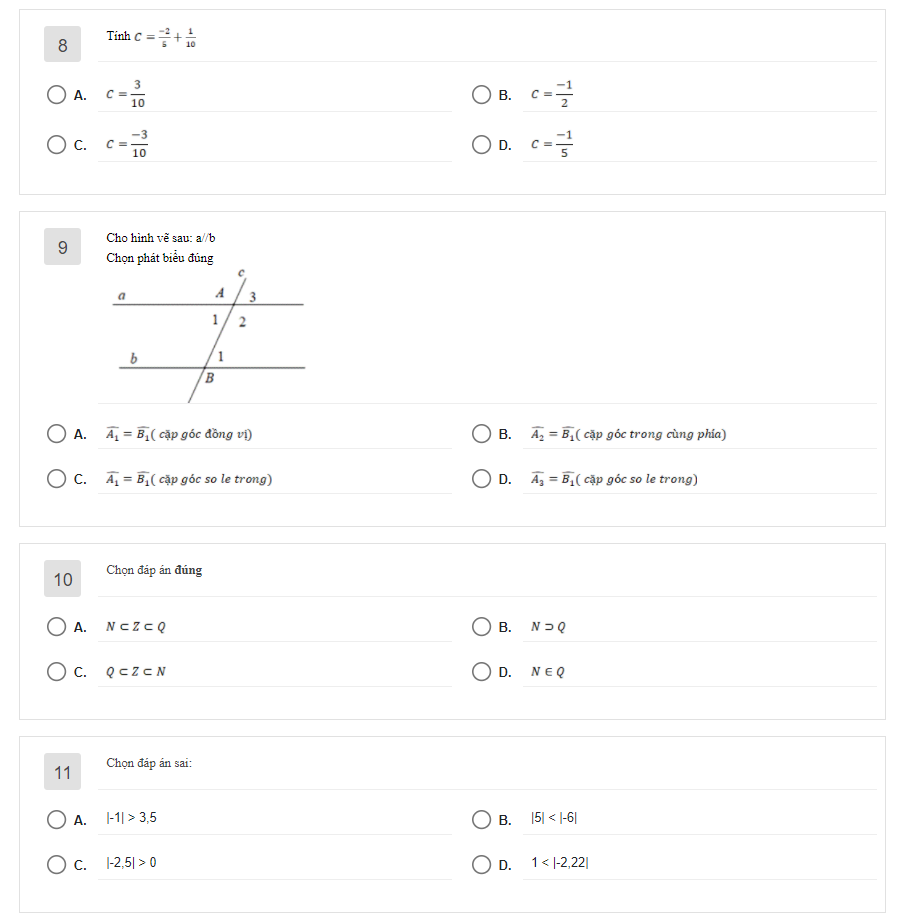
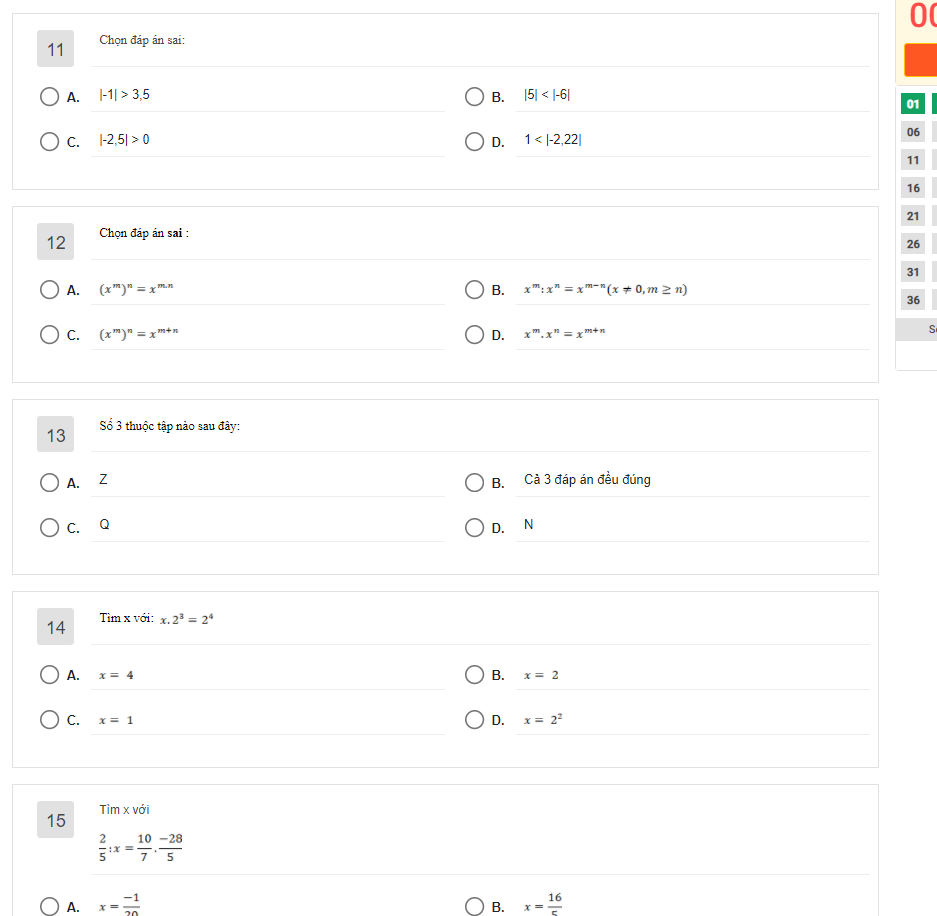
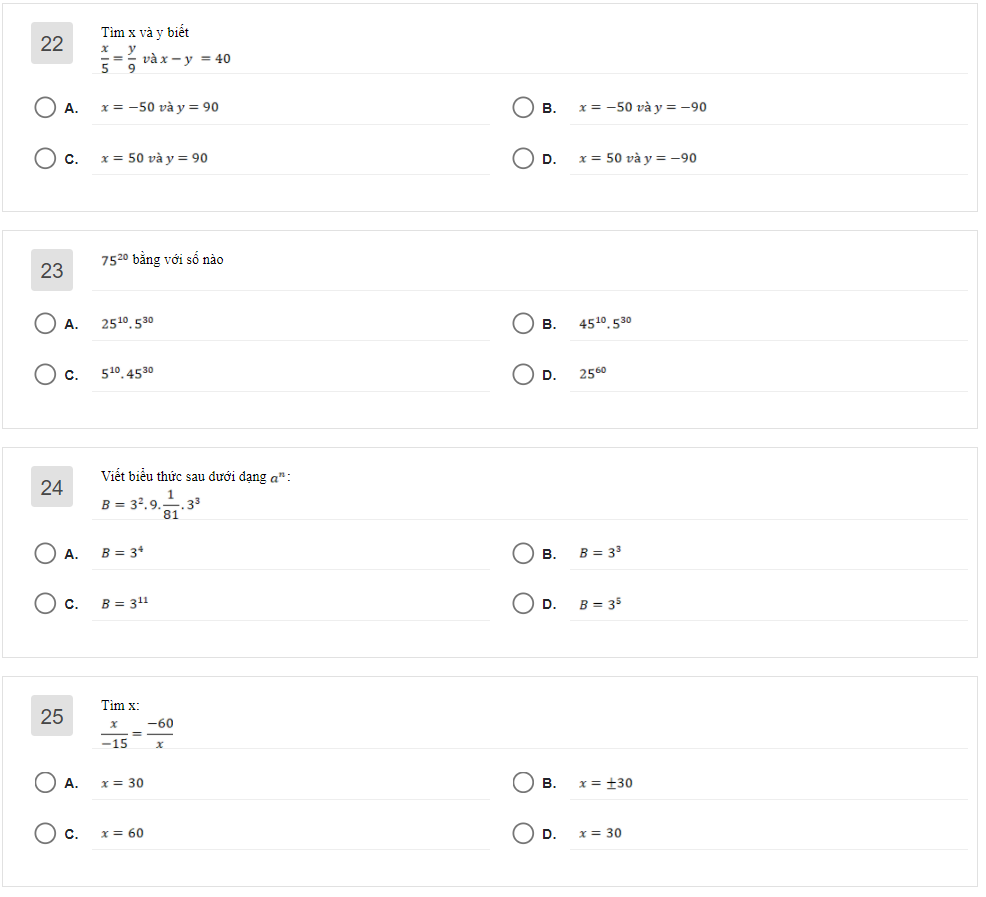
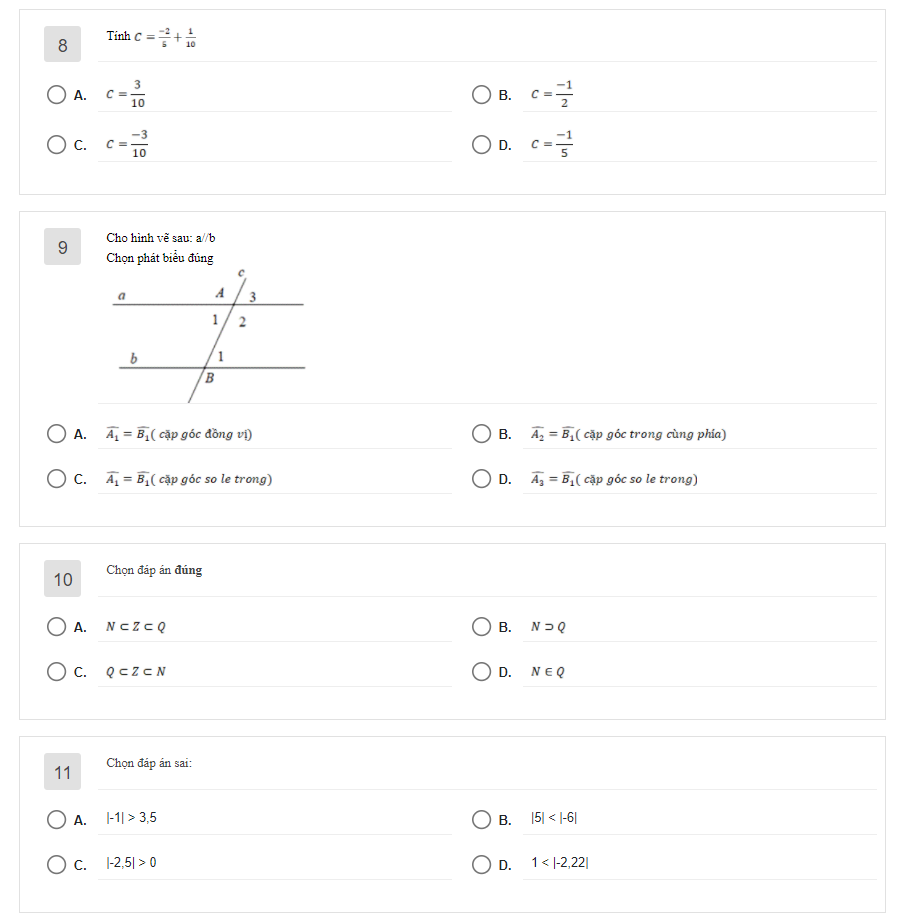
a)Xét tam giác ABM và tam giác DBM có:
BA=BD (gt)
góc ABM = góc DBM (vì BM là tia phân giác của góc ABC)
BM là cạnh chung
=> tam giác ABM = tam giác DBM (c.g.c)
=> góc BAM = góc BDM (hai góc tương ứng)
Mà góc BAM = 90 độ
=> góc BDM = 90 độ => MD vuông góc với BC
Vậy MD vuông góc với BC
b)Vì tam giác ABM = tam giác DBM (cmt)
=> AM = DM (hai cạnh tương ứng)
Xét tam giác AMH và tam giác DMC có:
góc MAH = góc MDC (=90 độ)
AM = DM (cmt)
góc AMH = góc DMC (hai góc đối đỉnh)
=> tam giác AMH = tam giác DMC (g.c.g)
d)Vì tam giác AMH = tam giác DMC (cmt)
=> HM = CM (hai cạnh tương ứng)
*Vì tam giác ABM = tam giác DBM (cmt) => góc AMB = góc DMB (hai góc tương ứng)
*Vì tam giác AMH = tam giác DMC (cmt) => góc AMH = góc DMC (hai góc tương ứng)
=>góc ABM + góc AMH = góc DMB + góc DMC
=> góc BMH = góc BMC
Xét tam giác BHM và tam giác BCM có
góc HBM = góc CBM (vì BM là tia phân giác của góc ABC)
BM là cạnh chung
góc BMH = góc BMC (cmt)
=> tam giác BHM = tam giác BCM (g.c.g)
=> BH = BC (hai cạnh tương ứng)
=> tam giác BHC cân tại B
=> góc BHK = góc BCK (hai góc tương ứng)
*Xét tam giác BHK và tam giác BCK có:
BH = BC (hai cạnh tương ứng)
góc BHK = góc BCK (cmt)
HK = CK (vì K là trung điểm của HC)
=> tam giác BHK = tam giác BCK (c.g.c)
=> góc HBK = góc CBK (hai góc tương ứng)
Mà tia BK nằm giữa tia BH và tia BC
=> BK là tia phân giác của góc HBC
Mà tia BM là tia phân giác của góc ABC hay góc HBC
=> tia BK và tia BM trùng nhau
=> 3 điểm B,M,K thẳng hàng
phần c tui cảm thấy hơi sai sai gì đó, mong bạn kiểm tra lại cái đề