ai giúp em với được không ạ
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
DD
0
NV
Nguyễn Việt Lâm
Giáo viên
6 tháng 8 2021
\(a=\dfrac{1}{9}.\left(999...9\right)=\dfrac{1}{9}.\left(100...0-1\right)=\dfrac{1}{9}\left(10^n-1\right)\)
\(b=100...0+5=10^n+5\)
\(\Rightarrow ab+1=\dfrac{1}{9}\left(10^n-1\right)\left(10^n+5\right)+1=\dfrac{1}{9}\left(10^{2n}+4.10^n+4\right)=\dfrac{1}{9}\left(10^n+2\right)^2\)
\(=\left(\dfrac{10^n+2}{3}\right)^2\)
Ta có: \(10\equiv1\left(mod3\right)\Rightarrow10^n\equiv1\left(mod3\right)\)
\(\Rightarrow10^n+2⋮3\)
\(\Rightarrow\dfrac{10^n+2}{3}\in Z\)
\(\Rightarrow\left(\dfrac{10^n+2}{3}\right)^2\) là SCP hay \(ab+1\) là SCP
9 tháng 9 2021
\(P=\left(x-y\right)^2+\left(x+y\right)^2-2\left(x-y\right)\left(x+y\right)-4x^2\\ P=\left(x-y-x-y\right)^2-4x^2\\ P=4y^2-4x^2=4\left(y-x\right)\left(x+y\right)\)
TH
1
29 tháng 12 2023
\(a^3+b^3+c^3=3abc\)
=>\(\left(a+b\right)^3+c^3-3ab\left(a+b\right)-3abc=0\)
=>\(\left(a+b+c\right)\left[\left(a+b\right)^2-c\left(a+b\right)+c^2\right]-3ab\left(a+b+c\right)=0\)
=>\(\left(a+b+c\right)\left(a^2+2ab+b^2-ac-bc+c^2-3ab\right)=0\)
=>\(a^2+b^2+c^2-ab-ac-bc=0\)
=>\(2a^2+2b^2+2c^2-2ab-2ac-2bc=0\)
=>\(\left(a^2-2ba+b^2\right)+\left(b^2-2cb+c^2\right)+\left(a^2-2ac+c^2\right)=0\)
=>\(\left(a-b\right)^2+\left(b-c\right)^2+\left(a-c\right)^2=0\)
=>\(\left\{{}\begin{matrix}a-b=0\\b-c=0\\a-c=0\end{matrix}\right.\Leftrightarrow a=b=c\)
\(A=\dfrac{a^{2023}}{b^{2023}}+\dfrac{b^{2023}}{c^{2023}}+\dfrac{c^{2023}}{a^{2023}}\)
\(=\dfrac{a^{2023}}{a^{2023}}+\dfrac{b^{2023}}{b^{2023}}+\dfrac{c^{2023}}{c^{2023}}\)
=1+1+1
=3
NV
1
10 tháng 10 2021
\(P=\dfrac{x^3-y^3}{x^2y-xy^2}-\dfrac{x^3+y^3}{x^2y+xy^2}-\left(\dfrac{x}{y}-\dfrac{y}{x}\right)\left(\dfrac{x+y}{x-y}-\dfrac{x-y}{x+y}\right)\)
\(=\dfrac{\left(x-y\right)\left(x^2+xy+y^2\right)}{xy\left(x-y\right)}-\dfrac{\left(x+y\right)\left(x^2-xy+y^2\right)}{xy\left(x+y\right)}-\dfrac{x^2-y^2}{xy}\cdot\dfrac{x^2+2xy+y^2-x^2+2xy-y^2}{\left(x-y\right)\left(x+y\right)}\)
\(=\dfrac{x^2+xy+y^2-x^2+xy-y^2}{xy}-\dfrac{\left(x-y\right)\left(x+y\right)}{xy}\cdot\dfrac{4xy}{\left(x-y\right)\left(x+y\right)}\)
\(=2-4=-2\)
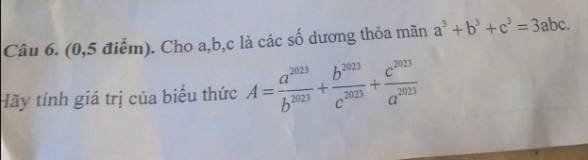
9, = \(\left(x^2\right)^2-\left(\dfrac{2}{5}y\right)^2=x^4-\dfrac{4}{25}y^2\)
10, = \(\left(\dfrac{x}{2}\right)^2-y^2=\dfrac{x^2}{4}-y^2\)