Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta chứng minh BĐT sau cho các số dương:
\(x^5+y^5\ge xy\left(x^3+y^3\right)\)
\(\Leftrightarrow x^5-x^4y+y^5-xy^4\ge0\)
\(\Leftrightarrow\left(x^4-y^4\right)\left(x-y\right)\ge0\)
\(\Leftrightarrow\left(x-y\right)^2\left(x+y\right)\left(x^2+y^2\right)\ge0\) (đúng)
Áp dụng:
\(\dfrac{a^5+b^5}{ab\left(a+b\right)}\ge\dfrac{ab\left(a^3+b^3\right)}{ab\left(a+b\right)}=\dfrac{a^3+b^3}{a+b}=a^2-ab+b^2\)
Tương tự và cộng lại:
\(VT\ge2\left(a^2+b^2+c^2\right)-\left(ab+bc+ca\right)=2-\left(ab+ca+ca\right)\)
\(VT\ge4-\left(ab+bc+ca\right)-2=4\left(a^2+b^2+c^2\right)-\left(ab+bc+ca\right)-2\)
\(VT\ge4\left(ab+bc+ca\right)-\left(ab+bc+ca\right)-2=3\left(ab+bc+ca\right)-2\) (đpcm)

\(3=ab+bc+ca\ge3\sqrt[3]{\left(abc\right)^2}\Rightarrow abc\le1\)
\(\dfrac{1}{1+a^2\left(b+c\right)}=\dfrac{1}{1+a\left(ab+ac\right)}=\dfrac{1}{1+a\left(3-bc\right)}=\dfrac{1}{1+3a-abc}=\dfrac{1}{3a+\left(1-abc\right)}\le\dfrac{1}{3a}\)
Tương tự và cộng lại:
\(VT\le\dfrac{1}{3a}+\dfrac{1}{3b}+\dfrac{1}{3c}=\dfrac{ab+bc+ca}{3abc}=\dfrac{3}{3abc}=\dfrac{1}{abc}\)

\(VT=\sqrt{\dfrac{a^2b^2}{c\left(a+b+c\right)+ab}}+\sqrt{\dfrac{b^2c^2}{a\left(a+b+c\right)+bc}}+\sqrt{\dfrac{a^2c^2}{b\left(a+b+c\right)+ac}}\\ VT=\sqrt{\dfrac{a^2b^2}{ac+ab+bc+c^2}}+\sqrt{\dfrac{b^2c^2}{a^2+ac+ab+bc}}+\sqrt{\dfrac{a^2c^2}{ab+bc+b^2+ac}}\\ VT=\sqrt{\dfrac{a^2b^2}{\left(c+a\right)\left(b+c\right)}}+\sqrt{\dfrac{a^2c^2}{\left(b+c\right)\left(a+b\right)}}+\sqrt{\dfrac{b^2c^2}{\left(a+b\right)\left(a+c\right)}}\)
Áp dụng BĐT Cauchy-Schwarz:
\(\Leftrightarrow\left\{{}\begin{matrix}\sqrt{\dfrac{b^2c^2}{\left(a+b\right)\left(a+c\right)}}\le\dfrac{\dfrac{bc}{a+b}+\dfrac{bc}{a+c}}{2}\\\sqrt{\dfrac{a^2c^2}{\left(a+b\right)\left(b+c\right)}}\le\dfrac{\dfrac{ca}{a+b}+\dfrac{ca}{b+c}}{2}\\\sqrt{\dfrac{a^2b^2}{\left(b+c\right)\left(a+c\right)}}\le\dfrac{\dfrac{ab}{b+c}+\dfrac{ab}{a+c}}{2}\end{matrix}\right.\)
\(\Rightarrow VT\le\dfrac{\left(\dfrac{bc}{a+b}+\dfrac{ca}{a+b}\right)+\left(\dfrac{ca}{b+c}+\dfrac{ab}{b+c}\right)+\left(\dfrac{bc}{a+c}+\dfrac{ab}{a+c}\right)}{2}\\ \Rightarrow VT\le\dfrac{a+b+c}{2}=\dfrac{2}{2}=1\)
Dấu \("="\Leftrightarrow a=b=c=\dfrac{2}{3}\)

Đặt vế trái là P
Ta có:
\(\dfrac{a}{b^3+ab}=\dfrac{a}{b\left(a+b^2\right)}=\dfrac{1}{b}-\dfrac{b}{a+b^2}\ge\dfrac{1}{b}-\dfrac{b}{2\sqrt{ab^2}}=\dfrac{1}{b}-\dfrac{1}{2\sqrt{a}}\ge\dfrac{1}{b}-\dfrac{1}{4}\left(\dfrac{1}{a}+1\right)\)
Tương tự và cộng lại:
\(P\ge\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}-\dfrac{1}{4}\left(\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}+3\right)\)
\(P\ge\dfrac{3}{4}\left(\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}\right)-\dfrac{3}{4}\ge\dfrac{3}{4}.\dfrac{9}{a+b+c}-\dfrac{3}{4}=\dfrac{3}{2}\) (đpcm)
Dấu "=" xảy ra khi \(a=b=c=1\)

\(1+\dfrac{9}{3\left(ab+bc+ca\right)}\ge1+\dfrac{9}{\left(a+b+c\right)^2}\ge2\sqrt{\dfrac{9}{\left(a+b+c\right)^2}}=\dfrac{6}{a+b+c}\)

\(\dfrac{a^2+bc}{b+c}=\dfrac{\left(a+b\right)\left(a+c\right)-a\left(b+c\right)}{b+c}=\dfrac{\left(a+b\right)\left(a+c\right)}{b+c}-a\)
\(\Rightarrow VT=\dfrac{\left(a+b\right)\left(a+c\right)}{b+c}+\dfrac{\left(a+b\right)\left(b+c\right)}{a+c}+\dfrac{\left(a+c\right)\left(b+c\right)}{a+b}-\left(a+b+c\right)\)
Mặt khác áp dụng \(x+y+z\ge\sqrt{xy}+\sqrt{yz}+\sqrt{zx}\)
\(\Rightarrow\dfrac{\left(a+b\right)\left(a+c\right)}{b+c}+\dfrac{\left(a+b\right)\left(b+c\right)}{a+c}+\dfrac{\left(a+c\right)\left(b+c\right)}{a+b}\ge a+b+b+c+a+c=2\left(a+b+c\right)\)
\(\Rightarrow VT\ge2\left(a+b+c\right)-\left(a+b+c\right)=a+b+c\) (đpcm)

Mẫu số to quá nên ko nghĩ ra cách giải đẹp mắt:
Dự đoán dấu "=" xảy ra tại \(a=b=c=1\), ta cần c/m: \(A\le\dfrac{3}{16}\)
Do \(\sum\dfrac{a+1}{a^2+1+10a+20}\le\sum\dfrac{a+1}{2a+10a+20}=\sum\dfrac{a+1}{12a+20}\)
Nên ta chỉ cần chứng minh: \(\sum\dfrac{a+1}{3a+5}\le\dfrac{3}{4}\Leftrightarrow\sum\left(\dfrac{3a+3}{3a+5}-1\right)\le\dfrac{9}{4}-3\)
\(\Leftrightarrow\sum\dfrac{1}{3a+5}\ge\dfrac{3}{8}\Leftrightarrow\dfrac{3\left(ab+bc+ca\right)+10\left(a+b+c\right)+25}{\left(3a+5\right)\left(3b+5\right)\left(3c+5\right)}\ge\dfrac{1}{8}\) (quy đồng)
\(\Leftrightarrow\dfrac{4\left(a+b+c\right)+3\left(ab+bc+ca+2\left(a+b+c\right)\right)+25}{27abc+45\left(ab+bc+ca+2\left(a+b+c\right)\right)-15\left(a+b+c\right)+125}\ge\dfrac{1}{8}\)
\(\Leftrightarrow\dfrac{4\left(a+b+c\right)+52}{27abc-15\left(a+b+c\right)+530}\ge\dfrac{1}{8}\)
\(\Leftrightarrow47\left(a+b+c\right)\ge27abc+114\)
Điều này đúng do:
\(9=2\left(a+b+c\right)+ab+bc+ca\le2\left(a+b+c\right)+\dfrac{1}{3}\left(a+b+c\right)^2\)
\(\Rightarrow\left(a+b+c-3\right)\left(a+b+c+9\right)\ge0\)
\(\Rightarrow a+b+c\ge3\)
Và: \(9=a+b+c+a+b+c+ab+bc+ca\ge9\sqrt[9]{a^4b^4c^4}\)
\(\Rightarrow abc\le1\)
\(\Rightarrow\left\{{}\begin{matrix}47\left(a+b+c\right)\ge141\\27abc+114\le27+114=141\end{matrix}\right.\) (đpcm)
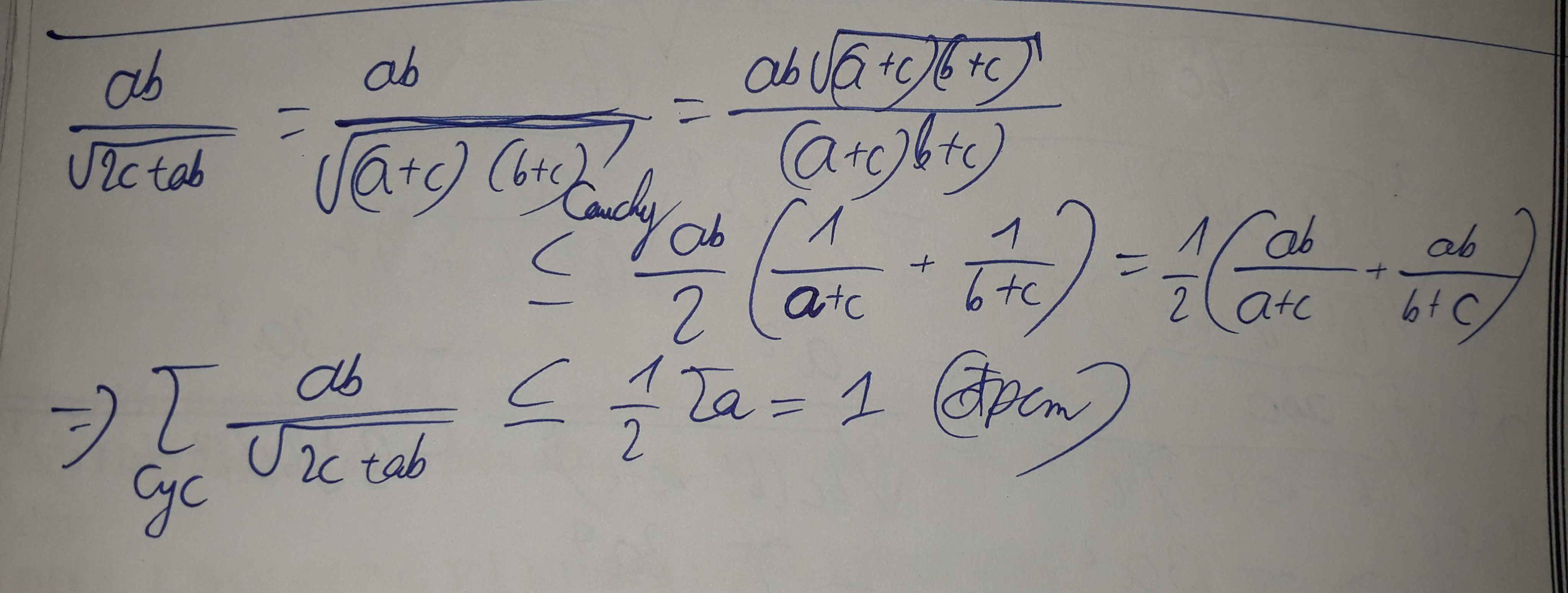
Đặt \(x=\sqrt{\dfrac{a}{bc}}\) ; \(y=\sqrt{\dfrac{b}{ca}}\) ; \(z=\sqrt{\dfrac{c}{ab}}\)
\(\Rightarrow a=\dfrac{1}{yz}\) ; \(b=\dfrac{1}{zx}\) ; \(c=\dfrac{1}{xy}\)
\(\Rightarrow xy+yz+zx=1\)
Khi đó, tồn tại một tam giác ABC sao cho:
\(x=tan\dfrac{A}{2}\) ; \(y=tan\dfrac{B}{2}\) ; \(z=tan\dfrac{C}{2}\)
Thay vào bài toán:
\(A=\dfrac{x^2}{1+x^2}+\sqrt{3}\left(\dfrac{y^2}{1+y^2}+\dfrac{z^2}{1+z^2}\right)\)
\(=\dfrac{tan^2\dfrac{A}{2}}{1+tan^2\dfrac{A}{2}}+\sqrt{3}\left(\dfrac{tan^2\dfrac{B}{2}}{1+tan^2\dfrac{B}{2}}+\dfrac{tan^2\dfrac{C}{2}}{1+tan^2\dfrac{C}{2}}\right)\)
\(=sin^2\dfrac{A}{2}+\sqrt{3}\left(sin^2\dfrac{B}{2}+sin^2\dfrac{C}{2}\right)\)
\(=\dfrac{1}{2}-\dfrac{1}{2}cosA+\dfrac{\sqrt{3}}{2}\left(2-cosB-cosC\right)\)
\(=\dfrac{1+2\sqrt{3}}{2}-\dfrac{1}{2}\left(cosA+\sqrt{3}cosB+\sqrt{3}cosC\right)\)
Xét \(B=cosA+\sqrt{3}\left(cosB+cosC\right)=cosA+2\sqrt{3}cos\dfrac{B+C}{2}cos\dfrac{B-C}{2}\)
\(\le cosA+2\sqrt{3}cos\dfrac{B+C}{2}=-2sin^2\dfrac{A}{2}+2\sqrt{3}sin\dfrac{A}{2}+1\)
Xét hàm \(f\left(t\right)=-2t^2+2\sqrt{3}sint+1\) với \(t\in\left(0;1\right)\)
\(f'\left(t\right)=-4t+2\sqrt{3}=0\Rightarrow t=\dfrac{\sqrt{3}}{2}\)
\(f\left(0\right)=1\) ; \(f\left(\dfrac{\sqrt{3}}{2}\right)=\dfrac{5}{2}\) ; \(f\left(1\right)=2\sqrt{3}-1\)
\(\Rightarrow B_{max}=\dfrac{5}{2}\)
\(\Rightarrow A\ge\dfrac{1+2\sqrt{3}}{2}-\dfrac{5}{4}=\dfrac{4\sqrt{3}-3}{4}\)