Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: \(=\dfrac{13\left(3-18\right)}{40\left(15-2\right)}=\dfrac{13}{15-2}\cdot\dfrac{-15}{40}=\dfrac{-3}{8}\)
b: \(=\dfrac{18\left(34-124\right)}{36\left(-17-13\right)}=\dfrac{1}{2}\cdot\dfrac{-90}{-30}=\dfrac{3}{2}\)
c: \(=\dfrac{3\left(\dfrac{1}{41}-\dfrac{4}{47}+\dfrac{9}{53}\right)}{4\left(\dfrac{1}{41}-\dfrac{4}{47}+\dfrac{9}{53}\right)}+\dfrac{\dfrac{-1}{4}\cdot\dfrac{-2}{3}-\dfrac{3}{4}:\dfrac{1}{6}}{\dfrac{3}{2}\cdot\left(\dfrac{-2}{3}-\dfrac{3}{4}\cdot\dfrac{-2}{3}\right)}\)
\(=\dfrac{3}{4}+\dfrac{\dfrac{2}{12}-\dfrac{9}{2}}{\dfrac{3}{2}\cdot\dfrac{-1}{6}}=\dfrac{3}{4}+\dfrac{-13}{3}:\dfrac{-3}{12}=\dfrac{3}{4}+\dfrac{13}{3}\cdot\dfrac{12}{3}\)
\(=\dfrac{3}{4}+\dfrac{156}{9}=\dfrac{217}{12}\)

p: \(F=\dfrac{1}{3}\left(\dfrac{3}{3\cdot6}+\dfrac{3}{6\cdot9}+\dfrac{3}{9\cdot12}+...+\dfrac{3}{30\cdot33}\right)\)
\(=\dfrac{1}{3}\left(\dfrac{1}{3}-\dfrac{1}{6}+\dfrac{1}{6}-\dfrac{1}{9}+...+\dfrac{1}{30}-\dfrac{1}{33}\right)\)
\(=\dfrac{1}{3}\cdot\dfrac{10}{33}=\dfrac{10}{99}\)
n: \(F=2\left(\dfrac{1}{2}-\dfrac{1}{4}+\dfrac{1}{4}-\dfrac{1}{6}+...+\dfrac{1}{2008}-\dfrac{1}{2010}\right)\)
\(=2\cdot\dfrac{502}{1005}=\dfrac{1004}{1005}\)
m: \(=\left(3-\dfrac{7}{3}+\dfrac{1}{4}\right):\left(4-\dfrac{31}{6}+\dfrac{9}{4}\right)\)
\(=\dfrac{36-28+3}{12}:\dfrac{48-62+27}{12}\)
\(=\dfrac{11}{13}\)

1: \(=\dfrac{15}{37}\cdot\dfrac{38}{41}-\dfrac{15}{37}\cdot\dfrac{74}{45}-\dfrac{38}{41}\cdot\dfrac{15}{37}-\dfrac{38}{41}\cdot\dfrac{82}{76}\)
\(=\dfrac{-2}{3}-1=-\dfrac{5}{3}\)
2: \(=\dfrac{47}{53}\cdot\dfrac{17}{3}-\dfrac{47}{53}\cdot\dfrac{53}{47}+\dfrac{17}{3}\cdot\dfrac{6}{17}-\dfrac{17}{3}\cdot\dfrac{47}{53}\)
\(=-1+2=1\)

a) \(5\dfrac{4}{23}.27\dfrac{3}{47}+4\dfrac{3}{47}.\left(-5\dfrac{4}{23}\right)\)
\(=5\dfrac{4}{23}.27\dfrac{3}{47}+\left(-4\dfrac{3}{47}\right).5\dfrac{4}{23}\)
\(=5\dfrac{4}{23}.\left[27\dfrac{3}{47}+\left(-4\dfrac{3}{47}\right)\right]\)
\(=5\dfrac{4}{23}.\left(27\dfrac{3}{47}-4\dfrac{3}{27}\right)\)
\(=5\dfrac{4}{23}.23\)
\(=\dfrac{119}{23}.23\)
\(=\dfrac{119}{23}\)
b) \(4.\left(\dfrac{-1}{2}\right)^3+\dfrac{3}{2}\)
\(=4.\dfrac{-1}{6}+\dfrac{3}{2}\)
\(=\dfrac{-4}{6}+\dfrac{3}{2}\)
\(=\dfrac{-2}{3}+\dfrac{3}{2}\)
\(=\dfrac{-4}{6}+\dfrac{9}{6}\)
\(=\dfrac{5}{6}\)
c) \(\left(\dfrac{1999}{2011}-\dfrac{2011}{1999}\right)-\left(\dfrac{-12}{1999}-\dfrac{12}{2011}\right)\)
\(=\dfrac{1999}{2011}-\dfrac{2011}{1999}-\dfrac{-12}{1999}+\dfrac{12}{2011}\)
\(=\left(\dfrac{1999}{2011}+\dfrac{12}{2011}\right)-\left(\dfrac{2011}{1999}+\dfrac{-12}{1999}\right)\)
\(=\dfrac{2011}{2011}-\dfrac{1999}{1999}\)
\(=1-1\)
\(=0\)
d) \(\left(\dfrac{-5}{11}+\dfrac{7}{22}-\dfrac{-4}{33}-\dfrac{5}{44}\right):\left(\dfrac{381}{22}-39\dfrac{7}{22}\right)\)
(đợi đã, mình chưa tìm được hướng làm...)

Bài 1:
a) \(\left(\dfrac{3}{8}+\dfrac{-3}{4}+\dfrac{7}{12}\right):\dfrac{5}{6}+\dfrac{1}{2}\)
\(=\left(\dfrac{9}{24}+\dfrac{-18}{24}+\dfrac{14}{24}\right):\dfrac{5}{6}+\dfrac{1}{2}\)
\(=\dfrac{5}{24}:\dfrac{5}{6}+\dfrac{1}{2}\)
\(=\dfrac{5}{24}.\dfrac{6}{5}+\dfrac{1}{2}\)
\(=\dfrac{1}{4}+\dfrac{1}{2}\)
\(=\dfrac{1}{4}+\dfrac{2}{4}\)
\(=\dfrac{3}{4}\)
b) \(\dfrac{1}{2}+\dfrac{3}{4}-\left(\dfrac{3}{4}-\dfrac{4}{5}\right)\)
\(=\dfrac{1}{2}+\dfrac{3}{4}-\dfrac{3}{4}+\dfrac{4}{5}\)
\(=\left(\dfrac{1}{2}+\dfrac{4}{5}\right)+\left(\dfrac{3}{4}-\dfrac{3}{4}\right)\)
\(=\dfrac{1}{2}+\dfrac{4}{5}\)
\(=\dfrac{5}{10}+\dfrac{8}{10}\)
\(=\dfrac{9}{5}\)
c) \(6\dfrac{5}{12}:2\dfrac{3}{4}+11\dfrac{1}{4}.\left(\dfrac{1}{3}+\dfrac{1}{5}\right)\)
\(=\dfrac{77}{12}:\dfrac{11}{4}+\dfrac{42}{4}.\left(\dfrac{1}{3}+\dfrac{1}{5}\right)\)
\(=\dfrac{77}{12}.\dfrac{4}{11}+\dfrac{42}{4}.\left(\dfrac{5}{15}+\dfrac{3}{15}\right)\)
\(=\dfrac{7}{3}+\dfrac{42}{4}.\dfrac{8}{15}\)
\(=\dfrac{7}{3}+\dfrac{14.2}{1.3}\)
\(=\dfrac{7}{3}+\dfrac{28}{3}\)
\(=\dfrac{35}{3}\)
d) \(\left(\dfrac{7}{8}-\dfrac{3}{4}\right).1\dfrac{1}{3}-\dfrac{2}{7}.\left(3,5\right)^2\)
\(=\left(\dfrac{7}{8}-\dfrac{6}{8}\right).\dfrac{4}{3}-\dfrac{2}{7}.12\dfrac{1}{4}\)
\(=\dfrac{1}{8}.\dfrac{4}{3}-\dfrac{2}{7}.\dfrac{49}{4}\)
\(=\dfrac{1}{6}-\dfrac{7}{2}\)
\(=\dfrac{1}{6}-\dfrac{21}{6}\)
\(=\dfrac{-10}{3}\)
e) \(\left(\dfrac{3}{5}+0,415-\dfrac{3}{200}\right).2\dfrac{2}{3}.0,25\)
\(=\left(\dfrac{3}{5}+\dfrac{83}{200}-\dfrac{3}{200}\right).\dfrac{8}{3}.\dfrac{1}{4}\)
\(=\left(\dfrac{120}{200}+\dfrac{83}{200}-\dfrac{3}{200}\right).\dfrac{8}{3}.\dfrac{1}{4}\)
\(=1.\dfrac{8}{3}.\dfrac{1}{4}\)
\(=\dfrac{2}{3}\)
f) \(\dfrac{5}{16}:0,125-\left(2\dfrac{1}{4}-0,6\right).\dfrac{10}{11}\)
\(=\dfrac{5}{16}:\dfrac{1}{8}-\left(\dfrac{9}{4}-\dfrac{3}{5}\right).\dfrac{10}{11}\)
\(=\dfrac{5}{16}.\dfrac{8}{1}-\left(\dfrac{45}{20}-\dfrac{12}{20}\right).\dfrac{10}{11}\)
\(=\dfrac{5}{2}-\dfrac{33}{20}.\dfrac{10}{11}\)
\(=\dfrac{5}{2}-\dfrac{3}{2}\)
\(=\dfrac{2}{2}=1\)
g) \(0,25:\left(10,3-9,8\right)-\dfrac{3}{4}\)
\(=\dfrac{1}{4}:\dfrac{1}{2}-\dfrac{3}{4}\)
\(=\dfrac{1}{4}.\dfrac{2}{1}-\dfrac{3}{4}\)
\(=\dfrac{1}{2}-\dfrac{3}{4}\)
\(=\dfrac{2}{4}-\dfrac{3}{4}\)
\(=\dfrac{-1}{4}\)
h) \(1\dfrac{13}{15}.0,75-\left(\dfrac{11}{20}+20\%\right):\dfrac{7}{3}\)
\(=\dfrac{28}{15}.\dfrac{3}{4}-\left(\dfrac{11}{20}+\dfrac{1}{5}\right):\dfrac{7}{3}\)
\(=\dfrac{7}{5}-\left(\dfrac{11}{20}+\dfrac{4}{20}\right):\dfrac{7}{3}\)
\(=\dfrac{7}{5}-\dfrac{3}{4}:\dfrac{7}{3}\)
\(=\dfrac{7}{5}-\dfrac{9}{28}\)
\(=\dfrac{196}{140}-\dfrac{45}{140}\)
\(=\dfrac{151}{140}\)
i) \(\dfrac{\left(\dfrac{1}{2-0,75}\right).\left(0,2-\dfrac{2}{5}\right)}{\dfrac{5}{9}-1\dfrac{1}{12}}\)
\(=\dfrac{\left(\dfrac{1}{1,25}\right).\left(\dfrac{1}{5}-\dfrac{2}{5}\right)}{\dfrac{5}{9}-\dfrac{13}{12}}\)
\(=\dfrac{\dfrac{1}{1,25}.\dfrac{-1}{5}}{\dfrac{20}{36}-\dfrac{39}{36}}\)
\(=\dfrac{\dfrac{-1}{6,25}}{\dfrac{-19}{36}}\)
k) \(\dfrac{\dfrac{2}{3}+\dfrac{2}{7}-\dfrac{1}{14}}{-1-\dfrac{3}{7}+\dfrac{3}{28}}\)
\(=\dfrac{\dfrac{2}{3}+\dfrac{2}{7}-\dfrac{2}{28}}{-\dfrac{3}{3}-\dfrac{3}{7}+\dfrac{3}{28}}\)
\(=\dfrac{2\left(\dfrac{1}{3}+\dfrac{1}{7}-\dfrac{1}{28}\right)}{\left(-3\right)\left(\dfrac{1}{3}+\dfrac{1}{7}-\dfrac{1}{28}\right)}\)
\(=-\dfrac{2}{3}\)
\(A=0,7.2\dfrac{2}{3}.20.0,375.\dfrac{5}{28}\)
\(A=\dfrac{7}{10}.\dfrac{8}{3}.20.\dfrac{3}{8}.\dfrac{5}{28}\)
\(A=\left(\dfrac{7}{10}.\dfrac{5}{28}\right).\left(\dfrac{8}{3}.\dfrac{3}{8}\right).20\)
\(A=\dfrac{1}{8}.1.20\)
\(A=\dfrac{20}{8}=\dfrac{5}{2}\)
\(B=\left(9\dfrac{30303}{80808}+7\dfrac{303030}{484848}\right)+4,03\)
\(B=\left(9\dfrac{3}{8}+7\dfrac{5}{8}\right)+4,03\)
\(B=\left[\left(9+7\right)+\left(\dfrac{3}{8}+\dfrac{5}{8}\right)\right]+4,03\)
\(B=\left(16+1\right)+4,03\)
\(B=17+4,03\)
\(B=21,03\)
\(C=\left(9,75.21\dfrac{3}{7}+\dfrac{39}{4}.18\dfrac{4}{7}\right).\dfrac{15}{78}\)
\(C=\left(\dfrac{39}{4}.\dfrac{150}{7}+\dfrac{39}{4}.\dfrac{130}{7}\right).\dfrac{15}{78}\)
\(C=\dfrac{39}{4}.\left(\dfrac{150}{7}+\dfrac{130}{7}\right).\dfrac{15}{78}\)
\(C=\dfrac{39}{4}.40.\dfrac{15}{78}\)
\(C=390.\dfrac{15}{78}\)
\(C=75\)

Ta có : \(\dfrac{3\left(\dfrac{1}{41}-\dfrac{4}{47}+\dfrac{9}{53}\right)}{4.\left(\dfrac{1}{41}-\dfrac{4}{47}+\dfrac{9}{53}\right)}=\dfrac{3}{4}\)
\(\dfrac{\dfrac{3}{41}-\dfrac{12}{47}+\dfrac{27}{53}}{\dfrac{4}{41}-\dfrac{16}{47}+\dfrac{36}{53}}\)
\(=\dfrac{3\times\left(\dfrac{1}{41}-\dfrac{4}{47}+\dfrac{9}{53}\right)}{4\times\left(\dfrac{1}{41}-\dfrac{4}{47}+\dfrac{9}{53}\right)}\)
\(=\dfrac{3}{4}\)

a)\(\dfrac{4}{2\cdot4}+\dfrac{4}{4\cdot6}+\dfrac{4}{6\cdot8}+...+\dfrac{4}{2008\cdot2010}\)
\(=2\left(\dfrac{2}{2\cdot4}+\dfrac{2}{4\cdot6}+\dfrac{2}{6\cdot8}+...+\dfrac{2}{2008\cdot2010}\right)\)
\(=2\left(\dfrac{1}{2}-\dfrac{1}{4}+\dfrac{1}{4}-\dfrac{1}{6}+...+\dfrac{1}{2008}-\dfrac{1}{2010}\right)\)
\(=2\left(\dfrac{1}{2}-\dfrac{1}{2010}\right)=2\cdot\dfrac{502}{1005}=\dfrac{1004}{1005}\)
b)\(\dfrac{\dfrac{3}{41}-\dfrac{12}{47}+\dfrac{27}{53}}{\dfrac{4}{41}-\dfrac{16}{47}+\dfrac{36}{53}}=\dfrac{3\left(\dfrac{1}{41}-\dfrac{4}{47}+\dfrac{9}{53}\right)}{4\left(\dfrac{1}{41}-\dfrac{4}{47}+\dfrac{9}{53}\right)}=\dfrac{3}{4}\)
a) gọi biểu thức đó là A
Ta có công thức \(\dfrac{a}{b.c}=\dfrac{a}{c-b}.\left(\dfrac{1}{b}-\dfrac{1}{c}\right)\)
Dựa vào công thức trên, ta có
\(A=\dfrac{4}{2}.\left(\dfrac{1}{2}-\dfrac{1}{4}+\dfrac{1}{4}-\dfrac{1}{6}+....+\dfrac{1}{2008}-\dfrac{1}{2009}\right)\)
\(A=\dfrac{4}{2}.\left(\dfrac{1}{2}-\dfrac{1}{2009}\right)\)
\(A=2.\left(\dfrac{2007}{4018}\right)=\dfrac{2007}{2009}\)
b) dễ quá bạn tự làm. (không phải mink không biết làm đâu nha)
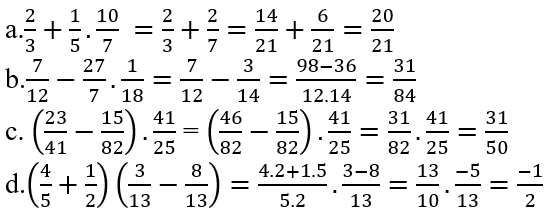
tính nhanh