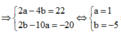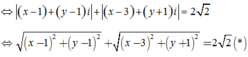Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

(P) tiếp xúc với (S) nên P và S phải có điểm chung duy nhất là M
thay tọa độ M vào các phương trình thử thì
Câu A đúng
Tìm \(\overline{z}\) biết :
a) \(z=1-i\sqrt{2}\)
b) \(z=-\sqrt{2}+i\sqrt{3}\)
c) \(z=5\)
d) \(z=7i\)

a) (3 - 5i) + (2 + 4i) = (3 + 2) + (-5i + 4i) = 5 - i.
b) (-2 - 3i) + (-1 - 7i) = (-2 - 1) + (-3i - 7i) = -3 - 10i
c) (4 + 3i) - (5 - 7i) = (4 - 5) + (3i + 7i) = -1 + 10i
d) (2 - 3i) - ( 5 - 4i) = (2 - 5) + (-3i + 4i) = -3 + i

Chọn D.
Giả sử z = x + yi có điểm biểu diễn là M(x; y).
Số phức z - 1có điểm biểu diễn A(x - 1; y) và z - 1 có điểm biểu diễn là B(x; y - 1).
Ta có
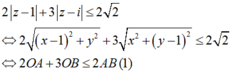
Mà 2OA + 3OB = 2OA + 2OB + OB ≥ 2 AB + OB (2)
Từ (1) và (2) suy ra 2AB + OB ≤ 2AB khi và chỉ khi B và O trùng nhau
Khi đó x; x = 0 và y = 1.
Khi đó z = i ⇒ |z| = 1.

đã hỏi thầy giáo và đã hiêu câu này. Quả thực đáp án A là đúng
Cảm ơn ai đang đã quan tâm đến.

Lời giải:

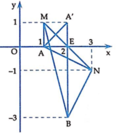
Trên mp tọa độ \(Oxy\) ta xét các điểm \(A(-2,1);B(4,7);C(1,-1)\). Tập hợp các điểm biểu diễn số phức $z$ là $M$
Theo bài ra ta có:
\(|z-(-2+i)|+|z-(4+7i)|=6\sqrt{2}\Leftrightarrow MA+MB=6\sqrt{2}\)
Mà \(AB=\sqrt{(-2-4)^2+(1-7)^2}=6\sqrt{2}\Rightarrow MA+MB=AB\)
Do đó điểm \(M\) nằm trên đoạn thẳng $AB$
Đề bài yêu cầu tìm max min của \(|z-(1-i)|\), tức là tìm max, min của đoạn \(MC\)
Dựa vào hình vẽ, suy ra \(MC_{\min}=d(C,AB)\).
Do biết tọa độ $A,B$ nên dễ dàng viết được PTĐT $AB$ là : \(y=x+3\)
\(\Rightarrow MC_{\min}=d(C,AB)=\frac{|1-(-1)+3|}{\sqrt{2}}=\frac{5\sqrt{2}}{2}\)
Vì \(M\) chỉ chạy trên đoạn $AB$ nên \(MC_{\max}=CA\) hoặc $CB$
Thấy \(CA< CB\Rightarrow CM_{\max}=CB=\sqrt{(4-1)^2+(7+1)^2}=\sqrt{73}\) khi \(M\equiv B\)
Vậy \(\left\{\begin{matrix} |z-1+i|_{\min}=\frac{5\sqrt{2}}{2}\\ |z-i+1|=\sqrt{73}\end{matrix}\right.\)