Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Công thức số hạng tổng quát \({u_n} = 5n,\;n \in {N^*}\).
b) Số hạng đầu \({u_1} = 5\), \({u_n} = {u_{n - 1}} + 5\)
Suy ra hệ thức truy hồi: \(\left\{ \begin{array}{l}{u_1}\; = 5\\{u_n} = {u_{n - 1}} + 5\end{array} \right.\)

a) Năm số hạng đầu của dãy số: 1; 3; 5; 7; 9.
b) Công thức biểu diễn số hạng \({u_n}\) theo số hạng \({u_{n - 1}}\) là: \({u_n} = {u_{n - 1}} + 2\;\left( {n \ge 2} \right)\).

a)Năm số hạng đầu: 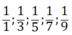
Số hạng tổng quát của dãy số: 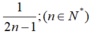
b)Năm số hạng đầu: 1;4;7;10;13
Số hạng tổng quát của dãy số: 3n + 1(n ∈ N)

Số hạng đầu của khai triển là u1 = u(1) = 13 = 1.
Số hạng cuối của khai triển là u5 = u(5) = 53 = 125.
Dãy số được viết dưới dạng khai triển là: 1; 8; 27; 64; 125.

a) Ta có: \({u_n} = 3n,\;\forall n \in {N^*}\).
b) Ta có: \({u_n} = 4n + 1,\forall n \in {N^*}\;\).

a) Năm số hạng đầu của dãy số là: \(u_1=1^2=1;u_2=2^2=4;u_3=3^2=9;u_4=4^2=16;u_5=5^2=25\).
Số hạng tổng quát của dãy số un là \(u_n=n^2\) với n ∈ ℕ.
b) Dạng khai triển của dãy số \(u_1=1,u_2=4,u_3=9,u_4=16,...u_n=n^2\) ...

a) \({u_1} = 1\)
\( \Rightarrow {u_2} = 2.1 = 2\)
\( \Rightarrow {u_3} = 3.2 = 6\)
\( \Rightarrow {u_4} = 4.6 = 24\)
\( \Rightarrow {u_5} = 5.24 = 120\)
b)
Ta có:
\({u_2} = 2 = 2.1 \)
\({u_3} = 6= 1.2.3 \)
\({u_4} = 24 = 1.2.3.4\)
\({u_5} = 120 = 1.2.3.4.5\)
\( \Rightarrow {u_n} = 1.2.3....n = n!\).

Chọn B.
- Ta có, u 1 = 5 và u n + 1 = 3 + u n nên dãy số là cấp số cộng với công sai d = 3, số hạng đầu u 1 = 5 .
- Do đó số hạng tổng quát của dãy số này là:
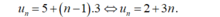
a) Ta có số hạng tổng quát của dãy số \({u_n} = 5n + 1\;\left( {n\; \in {N^*}} \right)\).
b) Các số hạng của dãy số là: 6; 11; 16; 21; 26.
Số hạng đầu của dãy số là: 6 và số hạng cuối của dãy số là 26.