Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

gọi số thứ nhất ; số thứ 2; số thứ 3 lần lượt là a; b; c
theo đề bài: \(\frac{a}{b}=\frac{14}{15};\frac{b}{c}=\frac{9}{10};2a+3b-4c=19\)
=> \(\frac{a}{14}=\frac{b}{15}\);
\(\frac{b}{9}=\frac{c}{10}\Rightarrow\frac{9}{15}.\frac{b}{9}=\frac{9}{15}.\frac{c}{10}\Rightarrow\frac{b}{15}=\frac{3c}{50}\)
=> \(\frac{a}{14}=\frac{b}{15}=\frac{3c}{50}=k\)
=> a = 14.k ; b = 15.k ; c = \(\frac{50}{3}\).k. Thay vào 2a + 3b - 4c = 19
=> 2.14k + 3.15.k - 4.\(\frac{50}{3}\).k = 19
<=> 84.k + 135.k - 200.k = 57 <=> 19.k = 57 <=> k = 3
Vậy a = 14.k = 14.3 = 42
b = 15.k = 15.3 = 45
c = 50/3 . k = 50/3 . 3 = 50
Vậy....

1) 15. 90 = 18.x => x =15.90 / 18 = 75
xong sớm hơn 90 - 75 =15 ngày
2) \(\frac{x}{3}=\frac{y}{5}=\frac{z}{7}=\frac{z-y}{7-5}=\frac{1}{2}\)
x =3/2
y=5/2
z=7/2
Tìm ba số r, s và t biết tỷ lệ r : s : t bằng 3 : 4 : 6 và số thứ nhất bé hơn số thứ ba 0,15 đơn vị.


Goi x,y,z lan luot la so thu nhat nhat, thu 2 va thu 3 can tim. Theo de ta co:
2x = 3 y = 5z => x lon nhat , z be nhat
Va: x-z = 72
=> \(\frac{x}{\frac{1}{2}}=\frac{y}{\frac{1}{3}}=\frac{z}{\frac{1}{5}}=\frac{x-z}{\frac{1}{2}-\frac{1}{5}}=\frac{72}{\frac{3}{10}}=240\)
=> y = 240 . 1/3 = 80
Vay: So thu 2 la 80

Gọi số thứ nhất và số thứ hai cần tìm là x và y.Theo đề bài ta có :
2x - y = 8
Mà x : y = 3 : 4 hoặc \(\frac{x}{y}=\frac{3}{4}\)hay \(\frac{x}{3}=\frac{y}{4}\)=> \(\frac{2x}{6}=\frac{y}{4}\)
Áp dụng tính chất dãy tỉ số bằng nhau ta có :
\(\frac{2x}{6}=\frac{y}{4}=\frac{2x-y}{6-4}=\frac{8}{2}=4\)
=> \(\hept{\begin{cases}\frac{x}{3}=4\\\frac{y}{4}=4\end{cases}}\Rightarrow\hept{\begin{cases}x=12\\y=16\end{cases}}\)
Vậy số thứ nhất là 12,số thứ hai là 16
Gọi số thứ nhất là x, số thứ hai là y ( x, y thuộc N )
Hai lần số thứ nhất hơn số thứ hai 8 đơn vị
=> 2x - y = 8 ( 1 )
Số thứ nhất và số thứ hai tỉ lệ với 3;4
=> x/3 = y/4 (2)
Từ (1) và (2) => 2x/6 = y/4 và 2x - y = 8
Áp dụng tính chất dãy tỉ số bằng nhau ta có :
\(\frac{2x}{6}=\frac{y}{4}=\frac{2x-y}{6-4}=\frac{8}{2}=4\)
2x/6 = 4 => 2x = 24 => x = 12
y/4 = 4 => y = 16
Vậy hai số cần tìm là 12 và 16

Gọi số máy cày của đội thứ nhất, đội thứ hai và đội thứ ba lần lượt là x , y , z x , y , z ∈ N *
Cùng cày thửa ruộng như nhau và năng suất các máy như nhau thì số máy cày và thời gian cày là hai đại lượng tỉ lệ nghịch. Do đó x, y, z tỉ lệ nghịch với 2,3,4 và x − z = 3.
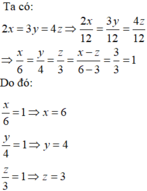
Vậy số máy cày của đội thứ nhât, đội thứ hai và đội thứ ba thứ tự là 6,4,3 máy.
Đáp án cần chọn là: C

Hatsune Miku này ai trả biết là dùng dãy tỉ số cách đều cái mình cần là cách làm
b, Gọi ba số cần tìm lần lượt là:
\(x;y;z\) theo bài ra ta có:
\(\dfrac{x}{4}\) = \(\dfrac{y}{5}\) = \(\dfrac{z}{6}\);
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
\(\dfrac{z}{6}\) = \(\dfrac{x}{4}\) = \(\dfrac{z-x}{6-4}\) = \(\dfrac{4}{2}\) = 2
z = 2 x 6 = 12
\(x\) = 2 x 4 = 8
\(\dfrac{y}{5}\) = 2 ⇒ y = 2 x 5 = 10
Vậy \(x\) = 8; y = 10; z = 12
a, Gọi ba số cần tìm lần lượt là: \(x\); y; z
Theo bài ra ta có: \(\dfrac{x}{3}\) = \(\dfrac{y}{5}\) = \(\dfrac{z}{7}\); z - 2\(x\) = 11
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
\(\dfrac{x}{3}\) = \(\dfrac{2x}{6}\) = \(\dfrac{z}{7}\) = \(\dfrac{z-2x}{7-6}\) = \(\dfrac{4}{1}\) = 4
\(x\) = 4x3 = 12; z = 4 x 7 = 28
\(\dfrac{y}{5}\) = 4 ⇒ y = 4x5 =20
Vậy \(x\) = 12; y = 20; z = 28