Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) \(log_50,5=-0,439677\)
c) \(In\left(\dfrac{3}{2}\right)=0,405465\)

a) \(1,2^{1,5}=1,314534\)
b) \(10^{\sqrt{3}}=53,957374\)
c) \(\left(0,5\right)^{-\dfrac{2}{3}}=1,587401\)

Từ 2020 đến 2050 sẽ là 2050-2020=30(năm)
Dân số VN vào năm 2050 sẽ là:
\(97.34\cdot e^{0.91\%\cdot30}\simeq127,90\)(triệu người)

a) Tập xác định của hàm số là \(D = \mathbb{R}\)
Do đó, nếu x thuộc tập xác định D thì –x cũng thuộc tập xác định D
Ta có: \(f\left( { - x} \right) = \sin \left( { - x} \right) = - \sin x = - f\left( x \right),\;\forall x\; \in \;D\)
Vậy \(y = \sin x\) là hàm số lẻ.
b)
\(x\) | \( - \pi \) | \( - \frac{{3\pi }}{4}\) | \( - \frac{\pi }{2}\) | \( - \frac{\pi }{4}\) | 0 | \(\frac{\pi }{4}\) | \(\frac{\pi }{2}\) | \(\frac{{3\pi }}{4}\) | \(\pi \) |
\(\sin x\) | \(0\) | \( - \frac{{\sqrt 2 }}{2}\) | \( - 1\) | \( - \frac{{\sqrt 2 }}{2}\) | 0 | \(\frac{{\sqrt 2 }}{2}\) | 1 | \(\frac{{\sqrt 2 }}{2}\) | 0 |
c) Từ đồ thị trên, ta thấy hàm số \(y = \sin x\) có tập xác định là \(\mathbb{R}\), tập giá trị là [-1;1] và đồng biến trên mỗi khoảng \(\left( { - \frac{\pi }{2} + k2\pi ;\frac{\pi }{2} + k2\pi } \right)\) và nghịch biến trên mỗi khoảng \(\left( {\frac{\pi }{2} + k2\pi ;\frac{{3\pi }}{2} + k2\pi } \right),\;k\; \in \;\mathbb{Z}.\)

\(v\left(t\right)=s'\left(t\right)=4\left[cos\left(2\pi t-\dfrac{\pi}{8}\right)\right]'\\ =-4\left(2\pi t-\dfrac{\pi}{8}\right)'sin\left(2\pi t-\dfrac{\pi}{8}\right)\\ =-8\pi sin\left(2\pi t-\dfrac{\pi}{8}\right)\)
Vận tốc của vật khi t = 5s là \(v\left(5\right)=-8\pi sin\left(10\pi-\dfrac{\pi}{8}\right)\approx9,6\left(m/s\right)\)

Đáp án D
Gọi A i là biến cố người thứ i phóng phi tiêu được 10 điểm. (i=1,2)
Gọi A là biến cố thỏa yêu cầu bài toán.
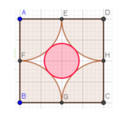
Dễ thấy
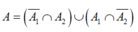
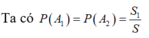
Trong đó
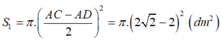
là diện tích hình tròn màu hồng S= 4.4 =16 là diện tích hình vuông ABCD.
Vậy
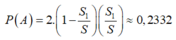
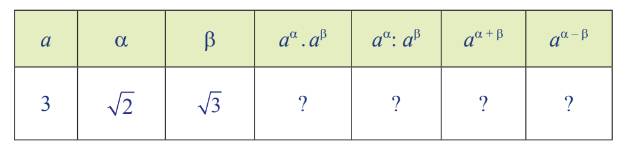





a)
\(\sqrt{2}\)
b) Nhận xét:
\(a^m\cdot a^n=a^{m+n};a^m:a^n=a^{m-n}\)