Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Tham khảo:
Đặt \(a = BC,b = AC,c = AB\)
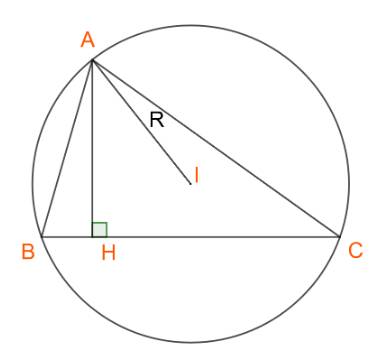
Ta có: \(\sin C = \frac{{AH}}{{AC}} = \frac{{{h_a}}}{b} \Rightarrow {h_a} = b.\sin C\)
Theo định lí sin, ta có: \(\frac{b}{{\sin B}} = 2R \Rightarrow b = 2R.\sin B\)
\( \Rightarrow {h_a} = 2R.\sin B.\sin C\)

Tham khảo:
a) Áp dụng hệ quả của định lí cosin, ta có:
\(\begin{array}{l}\cos A = \frac{{{b^2} + {c^2} - {a^2}}}{{2bc}};\cos B = \frac{{{a^2} + {c^2} - {b^2}}}{{2ac}}\\ \Rightarrow \left\{ \begin{array}{l}\cos A = \frac{{{{10}^2} + {{13}^2} - {8^2}}}{{2.10.13}} = \frac{{41}}{{52}} > 0;\\\cos B = \frac{{{8^2} + {{13}^2} - {{10}^2}}}{{2.8.13}} = \frac{{133}}{{208}} > 0\\\cos C = \frac{{{8^2} + {{10}^2} - {{13}^2}}}{{2.8.10}} = - \frac{1}{{32}} < 0\end{array} \right.\end{array}\)
\( \Rightarrow \widehat C \approx 91,{79^ \circ } > {90^ \circ }\), tam giác ABC có góc C tù.
b)
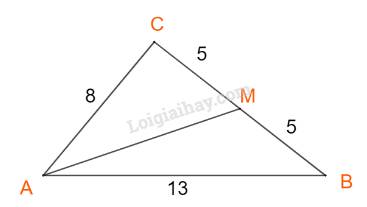
+) Áp dụng định lí cosin trong tam giác ACM, ta có:
\(\begin{array}{l}A{M^2} = A{C^2} + C{M^2} - 2.AC.CM.\cos C\\ \Leftrightarrow A{M^2} = {8^2} + {5^2} - 2.8.5.\left( { - \frac{1}{{32}}} \right) = 91,5\\ \Rightarrow AM \approx 9,57\end{array}\)
+) Ta có: \(p = \frac{{8 + 10 + 13}}{2} = 15,5\).
Áp dụng công thức heron, ta có: \(S = \sqrt {p(p - a)(p - b)(p - c)} = \sqrt {15,5.(15,5 - 8).(15,5 - 10).(15,5 - 13)} \approx 40\)
+) Áp dụng định lí sin, ta có:
\(\frac{c}{{\sin C}} = 2R \Rightarrow R = \frac{c}{{2\sin C}} = \frac{{13}}{{2.\sin 91,{{79}^ \circ }}} \approx 6,5\)
c)

Ta có: \(\widehat {BCD} = {180^ \circ } - 91,{79^ \circ } = 88,{21^ \circ }\); \(CD = AC = 8\)
Áp dụng định lí cosin trong tam giác BCD, ta có:
\(\begin{array}{l}B{D^2} = C{D^2} + C{B^2} - 2.CD.CB.\cos \widehat {BCD}\\ \Leftrightarrow B{D^2} = {8^2} + {10^2} - 2.8.10.\cos 88,{21^ \circ } \approx 159\\ \Rightarrow BD \approx 12,6\end{array}\)

Áp dụng định lí cosin trong tam giác ABC ta có:
\(B{C^2} = A{C^2} + A{B^2} - 2.AC.AB.\cos A\)
\( \Rightarrow \cos A = \frac{{A{C^2} + A{B^2} - B{C^2}}}{{2.AB.AC}} = \frac{{{7^2} + {6^2} - {8^2}}}{{2.7.6}} = \frac{1}{4}\)
Lại có: \({\sin ^2}A + {\cos ^2}A = 1 \Rightarrow \sin A = \sqrt {1 - {{\cos }^2}A} \)(do \({0^o} < A \le {90^o}\))
\( \Rightarrow \sin A = \sqrt {1 - {{\left( {\frac{1}{4}} \right)}^2}} = \frac{{\sqrt {15} }}{4}\)
Áp dụng định lí sin trong tam giác ABC ta có:\(\frac{{BC}}{{\sin A}} = 2R\)
\( \Rightarrow R = \frac{{BC}}{{2.\sin A}} = \frac{8}{{2.\frac{{\sqrt {15} }}{4}}} = \frac{{16\sqrt {15} }}{{15}}.\)
Vậy \(\cos A = \frac{1}{4};\)\(\sin A = \frac{{\sqrt {15} }}{4};\)\(R = \frac{{16\sqrt {15} }}{{15}}.\)

a) Áp dụng định lí cosin, ta có:
\(\begin{array}{l}{a^2} = {b^2} + {c^2} - 2bc.\cos A\\ \Leftrightarrow {a^2} = {8^2} + {5^2} - 2.8.5.\cos {120^ \circ } = 129\\ \Rightarrow a = \sqrt {129} \end{array}\)
Áp dụng định lí sin, ta có:
\(\begin{array}{l}\frac{a}{{\sin A}} = \frac{b}{{\sin B}} = \frac{c}{{\sin C}} \Rightarrow \frac{{\sqrt {129} }}{{\sin {{120}^ \circ }}} = \frac{8}{{\sin B}} = \frac{5}{{\sin C}}\\ \Rightarrow \left\{ \begin{array}{l}\sin B = \frac{{8.\sin {{120}^ \circ }}}{{\sqrt {129} }} \approx 0,61\\\sin C = \frac{{5.\sin {{120}^ \circ }}}{{\sqrt {129} }} \approx 0,38\end{array} \right. \Rightarrow \left\{ \begin{array}{l}\widehat B \approx 37,{59^ \circ }\\\widehat C \approx 22,{41^ \circ }\end{array} \right.\end{array}\)
b) Diện tích tam giác ABC là: \(S = \frac{1}{2}bc.\sin A = \frac{1}{2}.8.5.\sin {120^ \circ } = 10\sqrt 3 \)
c)
+) Theo định lí sin, ta có: \(R = \frac{a}{{2\sin A}} = \frac{{\sqrt {129} }}{{2\sin {{120}^ \circ }}} = \sqrt {43} \)
+) Đường cao AH của tam giác bằng: \(AH = \frac{{2S}}{a} = \frac{{2.10\sqrt 3 }}{{\sqrt {129} }} = \frac{{20\sqrt {43} }}{{43}}\)

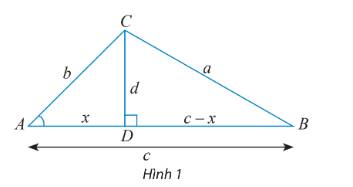
a) ? = x vì \(\cos A = \frac{{AD}}{{AC}} = \frac{x}{b} \Rightarrow ? = x.\)
b) Xét tam giác vuông BCD, ta có: \({a^2} = {d^2} + {(c + x)^2} = {d^2} + {x^2} + {c^2} + 2xc\) (1)
Xét tam giác vuông ACD, ta có: \({b^2} = {d^2} + {x^2} \Rightarrow {d^2} = {b^2} - {x^2}\) (2)
\(\cos A = - \cos \widehat {DAC} = - \frac{x}{b} \Rightarrow x = - b\cos A.\) (3)
Thay (2) và (3) vào (1), ta có: \({a^2} = {b^2} + {c^2} - 2bc\cos A\)
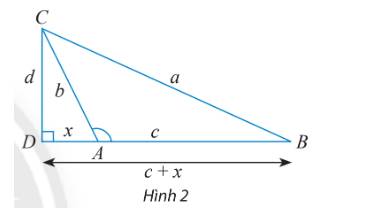
c) Ta có: \({a^2} = {b^2} + {c^2} - 2bc\cos A\)
Mà \(\widehat A = {90^o} \Rightarrow \cos A = \cos {90^o} = 0.\)
\( \Rightarrow {a^2} = {b^2} + {c^2}\)

Tham khảo:
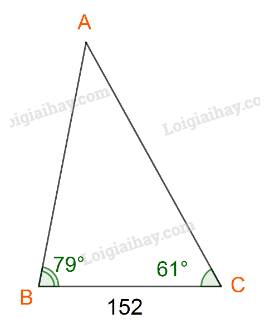
Đặt \(AB = c,AC = b,BC = a.\)
Ta có: \(a = 152;\widehat A = {180^o} - ({79^o} + {61^o}) = {40^o}\)
Áp dụng định lí sin, ta có:
\(\frac{a}{{\sin A}} = \frac{b}{{\sin B}} = \frac{c}{{\sin C}} = 2R\)
Suy ra:
\(\begin{array}{l}AC = b = \frac{{a.\sin B}}{{\sin A}} = \frac{{152.\sin {{79}^o}}}{{\sin {{40}^o}}} \approx 232,13\\AB = c = \frac{{a.\sin C}}{{\sin A}} = \frac{{152.\sin {{61}^o}}}{{\sin {{40}^o}}} \approx 206,82\\R = \frac{a}{{2\sin A}} = \frac{{152}}{{2\sin {{40}^o}}} \approx 118,235\end{array}\)
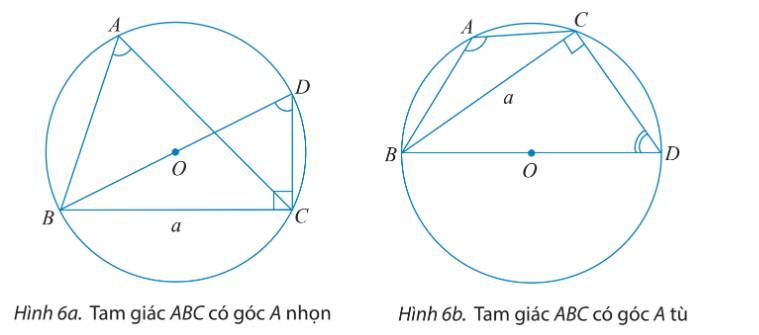
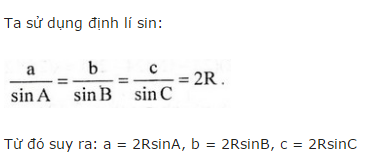
a) Tam giác BDC vuông tại C nên \(\sin \widehat {BDC} = \frac{{BC}}{{BD}} = \frac{a}{{2R}}.\)
b)
TH1: Tam giác ABC có góc A nhọn
\(\widehat {BAC} = \widehat {BDC}\) do cùng chắn cung nhỏ BC.
\( \Rightarrow \sin \widehat {BAC} = \sin \widehat {BDC} = \frac{a}{{2R}}.\)
TH2: Tam giác ABC có góc A tù
\(\widehat {BAC} + \widehat {BDC} = {180^o}\) do ABDC là tứ giác nội tiếp (O).
\( \Rightarrow \sin \widehat {BAC} = \sin ({180^o} - \widehat {BAC}) = \sin \widehat {BDC} = \frac{a}{{2R}}.\)
Vậy với góc A nhọn hay tù ta đều có \(2R = \frac{a}{{\sin A}}.\)
b) Nếu tam giác ABC vuông tại A thì BC là đường kính của (O).
Khi đó ta có: \(\sin A = \sin {90^o} = 1\) và \(a = BC = 2R\)
Do đó ta vẫn có công thức: \(2R = \frac{a}{{\sin A}}.\)